Дано треугольник abc ab=ac=15 см периметр треугольника = 48 см m n d - точки касания сторон и вписанной окружности найди а) длины отрезков bm и am -б) радиус вписанной окружности можно с решением подробным !
Другие вопросы по теме Геометрия
Популярные вопросы
- Қарахан мемлекетінің ішкі саясаты айтындарш...
1 - I)соединение с наибольшим содержанием серы 1. h₂s 2.h₂so₄ 3.so₂...
2 - Кратко что мы должны делать с мелким мусором?...
1 - Си если не затруднит переводcomplete jim s story with right words...
3 - 2. (a) определите явление а) горение спички b) испарение воды...
3 - Найти сторону квадрата площадью 144 кв см...
2 - Составе словосочитания гл+сущ+предлог со словами: документ, инструмент,...
2 - Пушка выстреливает снаряд под углом 45 градусов, определить скорость...
2 - Мне надо. а) 3(2x-5)= б)-5(2,8x-1,2)= в)0,2(7-4x)= г)-0,6(5+10x)...
1 - 1) в кастрюлю, содержащую 5 л воды при 10 градусов опустили кусок...
2
а) AM= 6, BM=9
б) r=4,5
Объяснение:
Для того чтобы не запутаться: n-BC, d-AC, m-AB.
Это на каких сторонах находятся точки.
1. Найдем третью сторону треугольника:
P=a+b+c
bc=48-(15+15)=18
2. Поскольку треугольник равнобедренный, точка касания, делит сторону BС на два равных отрезка:
BN=NC=9
3. По свойству касательных к окружности:
BN=NC=9
AM=AB-BM
(BM будет равно BN)
AM=15-9=6
4. Радиум можно будет найти по формуле площади:
r=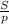
(p-полупериметр)
S=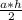
Ну или же:
(AD-высота, ее можно найти по теореме Пифагора: AD=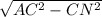 ; AD=
; AD=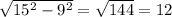 )
)
S=12*9=108
p=48:2=24
r=108:24=4,5