Дано точки : a(1; 1), b(1; 2), c(-2; 2), d(-3; 1). знайдіть кут між векторами ab і cd

Ответы

vlada3108 10.10.2020 16:28

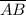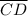Знайдемо координати векторів $\overline{AB}$ і $\overline{CD}$ :

$\overline{AB}=(1-1;2-1)=(0;1)\\\overline{CD}=(-3-(-2);1-2)=(-1;-1)$

Знайдемо їхні довжини (модулі):

$|\overline{AB}|=\sqrt{0^2+1^2}=1\\|\overline{CD}|=\sqrt{(-1)^2+(-1)^2}=\sqrt{2}$

Знайдемо їхній скалярний добуток через координати:

$\overline{AB} \cdot \overline{CD}=0 \cdot (-1)+1 \cdot (-1)=-1$

Тепер підставимо відомі значення в іншу формулу скалярного добутку, щоб знайти косинус кута (позначимо його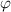 $\varphi$ ):

$\overline{AB} \cdot \overline{CD}=|\overline{AB}| \cdot| \overline{CD}| \cdot \cos \varphi=-1\\1 \cdot \sqrt 2 \cdot \cos \varphi = -1\\\cos \varphi=-\dfrac{1}{\sqrt 2}=-\dfrac{\sqrt 2}{2}\\\varphi=\dfrac{3 \pi}{4}$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

betmenduma 26.01.2020 19:34

если авсd - описанный четырехугольник с периметром 36 см и ав - cd =2 см ,то ав...

lydavika755 26.01.2020 21:31

(sin альфа*сos бета+cos альфа*sin бета) ^2+(sin альфа*cos бета *sin альфа *cos бета) ^2 ...

tsaturyansyuza 26.01.2020 21:26

1. пряма а перпендикулярна до площини β, а площина β паралельна прямій с. яким є взаємне розміщення прямих а і c? a. перпендикулярні.б. мимобіжні або паралельні.b. мимобіжні.г. паралельні.2....

спирина1 26.01.2020 21:26

Діагоналі рівнобічної трапеції є бісектрисами її гострих кутів. знайдіть середню лінію трапеції, якщо її периметр дорівнює 22 см. а діагональ ділить висоту, проведену з вершини тупого...

марян7878 26.01.2020 21:25

1. площина α перпендикулярна до прямої b, а пряма b паралельна прямій с. яке взаємне розміщення площини α і прямої c? a. паралельні.б. паралельні або перетинаються.b. перпендикулярні.г....

Nina2111 26.01.2020 21:23

Коло вписане в рівнобічну трапецію поділяє точкою дотику бічну сторону навідрізки завдовжки 8 см і 50 см. знайдіть радіус вписаного кола і основи трапеції....

Pavelteknik 26.01.2020 21:23

Стороны треугольника равны 9 14 корень из 151 найдите угол противолежащий средней стороне треугольника?...

nafikovmarat539 26.01.2020 21:21

Полностью расписать с доказательством и решением!...

Тетрадь22 22.05.2020 14:34

Начертить и назвать два произвольных треугольника. С линейки, транспортира и циркуля вписать окружность в первый треугольник. Описать окружность около второго треугольника....

Artemij08 22.05.2020 14:34

ДАНО ТРИКУТНИК АВС ЯКИЙ ВПИСАНИЙ В КОЛО СТОРОНА АБ ДИАМЕТР ЧЬОГО КОЛА ЗНАЙТЫ УТ ЦКЬОГО ТРЫКУТНЫЙ ЯКЩО КУТ А БИШЬШЕ КУТА Б НА 12 ГРАДУСИВ...

Дано точки : a(1; 1), b(1; 2), c(-2; 2), d(-3; 1). знайдіть кут між векторами ab і cd

Популярные вопросы