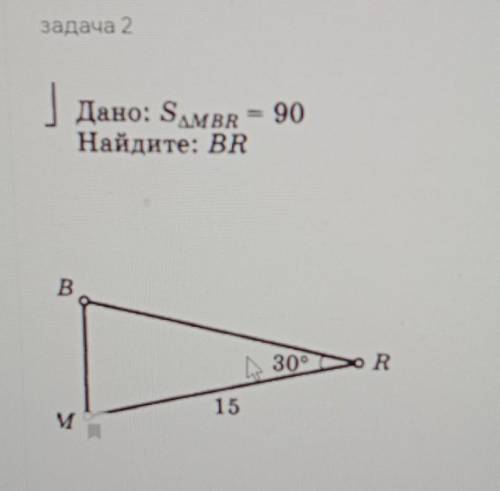
Дано: S MBR = 90
Найдите: BR
​

Чтобы решить эту задачу, мы можем использовать знания о сходственности треугольников. Существует основное свойство сходственных треугольников, которое гласит: если две стороны одного треугольника пропорциональны соответствующим сторонам в другом треугольнике, то эти треугольники сходственны.

В данной задаче у нас есть два треугольника: ABM и DRC. Мы знаем, что отрезки SB и SC являются высотами соответственно треугольников ABM и DRC. Заметим, что углы MBR и DRC равны и они оба прямые углы. Таким образом, треугольники ABM и DRC суть прямоугольные треугольники.

Теперь мы можем использовать свойство сходственных треугольников. Мы разделим соответствующие стороны треугольников ABM и DRC, чтобы найти пропорциональность:

SB / DR = BM / RC

Мы знаем, что SB = 90, так как это длина высоты BC в прямоугольном треугольнике ABM.
Также мы знаем, что BM = 12, так как это длина высоты AC в прямоугольном треугольнике ABM.

Подставим известные значения в пропорцию:

90 / DR = 12 / RC

Теперь нам нужно найти значения DR и RC, чтобы найти значение BR.
Мы можем использовать соотношение сторон в треугольнике ACD, чтобы найти DR и RC.
Отношение сторон в треугольниках ABM и DRC также будет равно отношению сторон в треугольнике ACD, так как треугольники ABM и DRC схожи с треугольником ACD.

В треугольнике ACD, отношение высоты SB к стороне AC равно 90 / 16.
Мы знаем, что SB = 90, так как это длина высоты BC в треугольнике ABM.
Мы знаем, что AC = 16, так как это сторона треугольника ACD.

Подставим известные значения в соотношение сторон:

90 / 16 = 12 / RC

Чтобы решить это уравнение относительно RC, мы можем умножить обе стороны на RC:

90 * RC = 16 * 12

Получаем:

90RC = 192

Теперь, чтобы найти значение RC, мы разделим обе стороны на 90:

RC = 192 / 90

Упростим значение:

RC = 2.13

Теперь, чтобы найти значение BR, мы можем использовать пропорцию:

SB / BR = BM / RC

Подставим известные значения:

90 / BR = 12 / 2.13

Чтобы решить это уравнение относительно BR, мы можем умножить обе стороны на BR:

90 = 12 * (BR / 2.13)

Далее, разделим обе стороны на 12:

7.5 = BR / 2.13

Умножим обе стороны на 2.13:

7.5 * 2.13 = BR

BR = 15.975

Таким образом, длина отрезка BR равна примерно 15.975.