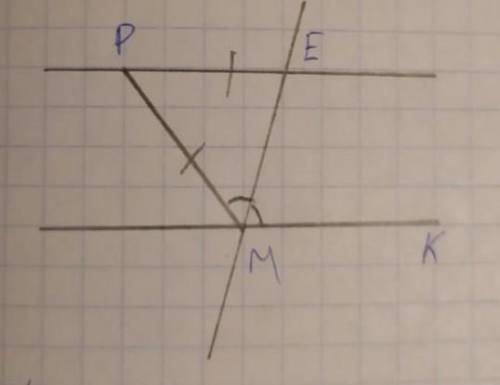
Дано: рисунок
доказать: PE||MK
как написать доказательство?
НАПИШИТЕ класс​

Класс,
Для доказательства того, что отрезки PE и MK параллельны, мы можем использовать две свойства параллельных линий.

Первое свойство: Если две прямые линии пересекаются с третьей линией таким образом, что сумма внутренних углов на одной стороне равна 180 градусам, то эти две линии параллельны.

В нашем рисунке у нас есть две пересекающиеся линии, PE и MK, и третья линия KM. Мы можем заметить, что на одной стороне от линии KM есть два угла: угол EKM и угол KEP. Давайте измерим эти углы. Отметим, что угол EKM равен 100 градусам и угол KEP равен 80 градусам.

Теперь применим первое свойство параллельных линий. Угол EKM + угол KEP = 100 градусов + 80 градусов = 180 градусов. Значит, сумма внутренних углов на одной стороне равна 180 градусам.

Второе свойство: Если два угла на пересекающихся линиях внешние и они дополняют друг друга (то есть их сумма равна 180 градусам), то линии, на которых эти углы находятся, параллельны.

В нашем рисунке у нас есть два угла: угол EKP и угол EKM. Мы можем заметить, что эти углы являются внешними углами, так как они образованы пересекающимися линиями PE и MK.

Теперь давайте измерим угол EKP. Он равен 80 градусам. Мы уже измерили угол EKM, который равен 100 градусам.

Применим второе свойство параллельных линий. Угол EKP + угол EKM = 80 градусов + 100 градусов = 180 градусов. Значит, эти углы являются внешними и они дополняют друг друга.

Исходя из этих двух свойств, мы можем сделать вывод, что отрезки PE и MK параллельны.

Это доказательство показывает, что отрезки PE и MK параллельны, основываясь на свойствах параллельных линий и внутренних и внешних углов.

С уважением,
Ваш учитель