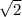Дано прямоугольный треугольник АВС, с угла А проведена биссектриса АК на сторону ВС, с точки К проведен перпендикуляр АК отрезок КN на сторону АВ, при этом АВ=3NB. Доказать ВК=АК
Другие вопросы по теме Геометрия
Популярные вопросы
- Найдите область определения функции y=квадратный корень из 3х-2/х+2...
3 - Ищу песню с мелодией lay down, stay down ! вдруг кто знает, исполняет рэп-!...
1 - Зачеркните лишнее слово в каждой группе.а)сеть сыновья, ,сосулька,сибирь .б)обьявление,вьюга,съёжился,подьзд,в)илья,татьяна,ольга,дарья...
2 - Вв одной молекуле днк нуклеотидов с тимином- 22%. определить нуклеотиды с цитозином,...
3 - Автомобиль,масса которого 800 кг,тормозит с силой 2 кн.время торможения до полной...
3 - Один из множителей произведения (8x+15y)(34x-43y) делится на 7. докажите что...
2 - Построить треугольник у которого 1 угол 80 градусов, прилежащяя сторона 3 см....
1 - Розберіть займенники як частину мови: та,яка,собі,свої,мені, ніким....
2 - V-? s-? если a-45см b-34см c-5дм переведи в дм...
2 - Подробный пересказ. рассказ черепаха толстова...
1
Объяснение:
Не уверен, но вариант такой:
Т.к. АВ=3NB, то AN=2NB, следовательно AN в два раза больше NB, а значит углы напроив этих сторон отличаются в два раза и следовательно угол BKN в два раза меньше угла NKA (который 90 град), получаем, что угол NKB равен 45 град.
Тогда угол AKC 180-90-45 = 45 град.
Тогда угол KAC 180-90-45 = 45 град. Значит треугольник АКС прямоугольный равнобедренный и АС=СК и так как АК биссектриса, то СК=ВК и = АС.
Для прямоугольного треугольника АКС получаем
квадрат АК= квадрату АС + квадрат КС
квадрат АК = квадрат ВК + квадрат ВК
АК = ВК х