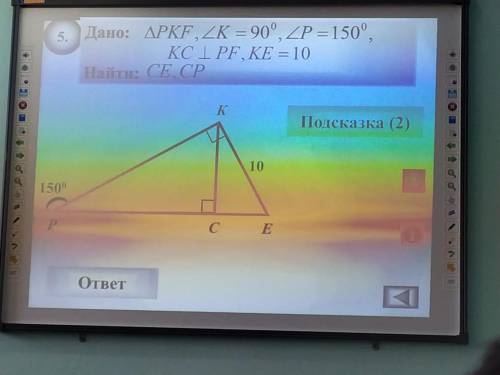
Дано: △PKF, ∠K=90°, ∠P=150°,

KC ⊥ PF, KE = 10

Найти: CE, CP

△PKF, ∠K=90°, ∠P=150°,

KC ⊥ PF, KE = 10

Найти: CE, CP

Дано: △PKF, ∠K=90°, ∠P=150°,

KC ⊥ PF, KE = 10

Найти: CE, CP

Дано: △PKF, ∠K=90°, ∠P=150°,

KC ⊥ PF, KE = 10

Найти: CE, CP

Дано: △PKF, ∠K=90°, ∠P=150°,

KC ⊥ PF, KE = 10

Найти: CE, CP

Объяснение:

Для решения данной задачи нам понадобятся знания о геометрических свойствах треугольника, а также о теореме Пифагора.

Дано, что ∠K = 90° и ∠P = 150°. Значит, в треугольнике △PKF угол K прямой (90°) и угол P больше 90°, что делает треугольник △PKF тупоугольным.

Также дано, что KC ⊥ PF, т.е. отрезок KC является высотой, опущенной из вершины K треугольника △PKF на сторону PF.

Из этого следует, что треугольник △KPC будет прямоугольным, а отрезок KC будет являться его гипотенузой.

Теперь перейдем к нахождению длин отрезков CE и CP.

Для начала, найдем длину отрезка CP.

Из прямоугольного треугольника △KPC известна длина отрезка KE, равная 10.

Теперь воспользуемся теоремой Пифагора, которая гласит, что в прямоугольном треугольнике с катетами a и b, и гипотенузой c, выполнено следующее соотношение: a^2 + b^2 = c^2.

В нашем случае a = KE = 10 (длина отрезка KE), b = CE (длина отрезка CE) и c = CP (длина отрезка CP).

Применяя теорему Пифагора к нашему треугольнику △KPC, получаем следующее уравнение: KE^2 + CE^2 = CP^2.

Подставляя известные значения, получаем: 10^2 + CE^2 = CP^2.

Теперь решим это уравнение относительно CP.

Вычитаем 10^2 (100) из обеих сторон уравнения: CE^2 = CP^2 - 100.

Так как нам нужно найти значение CP, оставим только его выражение в уравнении: CP^2 = CE^2 + 100.

Далее, возведем обе стороны уравнения в квадрат, чтобы избавиться от квадратных корней.

Получаем: CP^4 = (CE^2 + 100)^2.

Теперь найдем значение отрезка CE.

Зная, что △PKF является тупоугольным треугольником, можем вычислить угол ∠F, используя свойство суммы углов треугольника: ∠F = 180° - 90° - 150° = -60°.

Однако, угол не может быть отрицательным, поэтому примем ∠F = 60°.

Теперь можем находить длины отрезков CE и CP с использованием тригонометрических функций.

Обратимся к треугольнику △KCE.

В данном треугольнике у нас известны значения двух углов (∠C = 90° и ∠E = 60°) и одной стороны (KE = 10), поэтому можем использовать функцию синуса для нахождения отрезка CE.

Формула для синуса треугольника с неизвестной стороной a и соответствующим углом A выглядит следующим образом: sin(A) = a / c, где c - гипотенуза треугольника.

В нашем случае A = ∠E = 60°, a = CE (неизвестная сторона) и c = KE = 10.

Подставляя известные значения, получаем: sin(60°) = CE / 10.

Зная, что sin(60°) равен √3 / 2, можем решить это уравнение относительно CE: √3 / 2 = CE / 10.

Умножаем обе стороны уравнения на 10: 10 * √3 / 2 = CE.

Таким образом, получаем значение отрезка CE: CE = 5√3.

Теперь, чтобы найти значение отрезка CP, подставим найденное значение CE в уравнение: CP^4 = (5√3)^2 + 100.

Упрощаем выражение: CP^4 = 75 + 100.

Складываем числа: CP^4 = 175.

Для получения значения CP избавимся от степени 4, извлекая корень четвертой степени: CP = √(175).

Таким образом, мы нашли значения отрезков CE и CP.

CE = 5√3 и CP = √(175).

Ответ: CE = 5√3 и CP = √(175).