.(Дано основание прямоугольной призмы квадрат, радиус окружности вписанной в основание в 2 раза меньше радиуса окружности описанной около боковой грани призмы. площадь боковой грани 4 корня из 3.найти площадь поверхности
фигуры).
Другие вопросы по теме Геометрия
Популярные вопросы
- ЖАЗЫЛЫМ 9 -тапсырма. Төменде Фогг пен Паспартудың жүрген аты түсіп қалған. Соны...
3 - 7-тапсырма. Қарамен берілген сөздерді есімдіктермен ауыстырып жазыңдар. 1. Су...
2 - Найдите 2 предложения Present Voice....
2 - Рассмотри рисунок и определи,верны ли равенства...
1 - на вопросы ответить, которые галочкой помечены...
1 - еи (ею) ИМ ИМИ П.П. о ком? о чём? о нём О ней О нём О НИК 7. Выпиши местоимения...
3 - история россии 6 класс параграф 3 конспект...
1 - (c) Выберете одно верное утверждение, определенное в задание 1(b) и опишите взаимосвязь...
2 - 1.Ақан сері Ермеймен тауының етегіндегі кімнің асына келді? 2.Осы кезде бәйгеге...
3 - Основи ВС і AD трапеції ABCD дорівнюють відповідно 28 см і 63 см, кутАВС=кутACD....
2
Пусть сторона квадрата основания равна а, длина бокового ребра равна b.
Тогда радиус вписанной в квадрат окружности равен а/2. А радиус описанной около прямоугольника (axb) окружности равен (1/2)*кор(a^2+b^2). Кроме того площадь боковой грани равна ab.
В итоге получим систему:
Решим систему и найдем сторону квадрата основания:
Площадь основания:
Sосн = a^2 = 4.
Площадь боковой поверхности:
Sбок =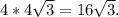
Искомая площадь полной поверхности:
S = 2Sосн + Sбок =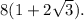
ответ: