Дано: <1=54°
m||n, k- секущая
Найти <2, <3, <4
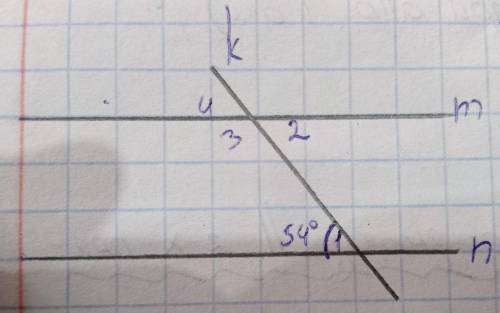
Другие вопросы по теме Геометрия
Популярные вопросы
- По татарскому языку сочинение на тему туган телем, иркэ голем...
2 - Put the right form of infinitive (with or without to). 1. i‘ve never been...
1 - Кто является героем преданий? (вопрос лёгкий просто лень искать)...
3 - №4 в каком словосочетании главным является первое слово? 1. по-настоящему...
3 - Найдите значение выражения 4x-0,3y,если x=-0,9 и y=0,7»...
2 - Опишите внешность человека позднего палеолита...
1 - Вцентре усадьбы растут густые кусты шиповника, жасмина, сирени, дикого винограда....
2 - Скласти речення про осінь або парк зі словами золотий, сріблястий, сіється,...
1 - Что означает слово глашатай в произведении никита кожемяка ?...
2 - Напишите выдуманную, мини как появилась нота соль!...
2
Чтобы решить эту задачу, мы будем использовать следующие свойства геометрических фигур:
1) Когда прямые m и n параллельны и пересекаются с прямой k, образуются коаксиальные углы (параллельные углы). Это значит, что углы, образованные прямыми m и k, а также прямыми n и k, равны между собой.
2) Когда касательная и секущая пересекаются на окружности, угол, образованный секущей и хордой, равен половине угла, образованного этой хордой и касательной, взятого на дуге, ограниченной хордой.
Теперь давайте решим задачу!
1) Найдем угол <2. Из свойства 1, угол, образованный прямыми m и k, равен углу <1 (54°). Таким образом, <2 = 54°.
2) Найдем угол <3. Из свойства 1, угол, образованный прямыми n и k, равен углу <1 (54°). Таким образом, <3 = 54°.
3) Найдем угол <4. Из свойства 2, угол, образованный секущей k и хордой nm, равен половине угла, образованного хордой nm и касательной. Угол <4 равен половине угла, образованного дугой om, исходящей из центра окружности, и дугой mn, также исходящей из центра окружности.
Чтобы найти этот угол, нам нужно узнать угол, образованный центральной дугой om, исходящей из центра окружности. Обозначим этот угол как x.
Угол x равен углу, образованному хордой nm и касательной tm, так как они охватывают одну и ту же дугу om и имеют общую точку приложения на окружности.
Теперь у нас есть два треугольника, в которых угол x является общим углом, и у нас есть сторона nm, которая в этих треугольниках является одинаковой (так как это хорда).
Таким образом, эти два треугольника будут подобными (по признаку общей стороны и общего угла). Это значит, что отношение сторон nm и tm в этих треугольниках будет равно отношению других сторон треугольников.
nm/tm = nm/om
nm/tm = 1/2 (по свойству 2)
Таким образом, отношение nm и tm равно 1/2.
Теперь нам известно, что углы треугольника pom равны 90° и 2х, поэтому сумма их углов равна 180°.
2х + 90° + <4 = 180°
2х + <4 = 180° - 90°
2х + <4 = 90°
Так как мы знаем, что отношение nm и tm равно 1/2, а угол, образованный хордой nm и касательной tm равен углу x, то можно записать следующее:
<4 = x (как угол, образованный хордой nm и касательной tm)
2х + <4 = 90°
2х + x = 90°
3х = 90°
x = 30°
Теперь мы знаем, что угол x равен 30°. Подставляем это значение в уравнение:
2х + <4 = 90°
2 * 30° + <4 = 90°
60° + <4 = 90°
<4 = 90° - 60°
<4 = 30°
Таким образом, угол <4 равен 30°.
Итак, ответ: <2 = 54°, <3 = 54° и <4 = 30°.