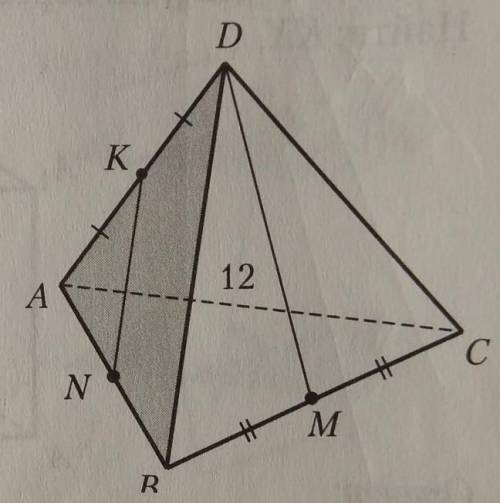
Дано: KN||DB, пл. KNX||DM, где X ∈ AC, AC=12.
Найти: AX.​​

Дано, что KN || DB, то есть прямые KN и DB параллельны. Поэтому у этих прямых соответственные углы равны. Имеем два соответственных угла: угол KNI и угол MDB.
Также, дано, что плоскость KNX || DM, то есть плоскости KNX и DM параллельны. Поэтому прямые KNX и DM пересекаются, образуя прямую NM, и у них соответственные углы равны. Имеем два соответственных угла: угол KNX и угол DNM.

Задача состоит в нахождении длины отрезка AX.

Рассмотрим треугольники KNI и NAX.
У этих треугольников угол KNI и гипотенуза KN соответственно равны углу NAX и гипотенузе NA. Так как углы этих треугольников равны, а гипотенузы имеют одинаковое значение, то эти треугольники подобны по первому признаку подобия (по углам).

Также рассмотрим треугольники DMN и AXM.
У этих треугольников угол DMN и гипотенуза DM соответственно равны углу AXM и гипотенузе AM. Так как углы этих треугольников равны, а гипотенузы имеют одинаковое значение, то эти треугольники подобны по первому признаку подобия (по углам).

Таким образом, треугольники KNI и NAX подобны, а треугольники DMN и AXM также подобны.

Мы можем использовать свойство подобных треугольников: соответствующие стороны таких треугольников пропорциональны. То есть, если обозначить длины сторон треугольников, то будет верно следующее соотношение:

KN/NA = NI/AX

DM/AM = MN/XM

Теперь давайте найдем нужные величины.

У нас дано, что KN || DB, поэтому углы KNI и MDB равны. Мы также знаем, что KNX || DM, поэтому углы KNX и DNM равны. Это значит, что углы KNI, MDB, KNX и DNM равны между собой.

Таким образом, угол NAX равен сумме углов KNX и DNM. Из условия задачи мы знаем, что KNX || DM, а значит угол KNX равен углу DNM. Значит, угол NAX равен удвоенному углу KNX (или удвоенному углу DNM).

Для нахождения значения угла KNX воспользуемся свойством, что сумма углов треугольника равна 180 градусам. Угол KNX равен 180 минус суммы углов KNI и INX (так как NI прямая и KnI + INX = 180). Угол KNI равен углу MDB, поэтому угол KNX равен 180 минус суммы углов MDB и INX (так как KnI + INX = KNX и KNX + MDB = 180).

Так как угол KNX равен углу DNM, то мы получаем уравнение:

180 - MDB - INX = DNM

180 -x - INX = x

2x = 180

x = 180/2

x = 90

Теперь мы можем подставить найденное значение x в уравнение KNX + MDB = 180:

90 + MDB = 180

MDB = 180 - 90

MDB = 90

У нас есть два угла треугольника, равные 90 градусов, что означает, что треугольник KNX прямоугольный. Значит мы можем воспользоваться теоремой Пифагора. Имеем:

MN^2 + NX^2 = MX^2

MN^2 + (12 - X)^2 = (AX + 12)^2

Из сотношения DM/AM = MN/XM получаем DM = MN * AM / XM

MD = (12 * AX) / XM

MN = DM - DN
= (12 * AX) / XM - 12

Подставим найденное значение MN в уравнение:

(12 * AX) / XM - 12 + (12 - X)^2 = (AX + 12)^2

Теперь, используя уравнение, мы можем решить его относительно AX. Для этого необходимо раскрыть скобки, собрать все слагаемые с AX в левую часть, а остальные слагаемые с X переместить в правую часть, и затем перенести все слагаемые без переменной в другую сторону уравнения.

Сложим (12 * AX) / XM - 12 и (12 - X)^2, и учтем, что (AX + 12)^2 = AX^2 + 24AX + 144:

(12 * AX) / XM - 12 + (12 - X)^2 = AX^2 + 24AX + 144

Теперь переместим все слагаемые с X в правую часть:

(12 * AX) / XM - AX^2 - 24AX = AX^2 + 144 - 12 + (12 - X)^2

Общий знаменатель XM поменяет расположение частей с помощью общего знаменателя:

12 * AX - XM * AX^2 - 24 * AX = AX^2 * XM + 144 * XM - 12 * XM + XM * (12 - X)^2

Теперь соберем все слагаемые с AX в левой части:

12 * AX - XM * AX^2 - 24 * AX - AX^2 * XM = 144 * XM - 12 * XM + XM * (12 - X)^2

Перенесем все слагаемые без переменной в правую часть:

XM * (12 - X)^2 + XM * AX^2 + 12 * XM + 24 * AX + AX^2 * XM = 12 * AX

Попробуем это упростить. Фокусируемся на левой части:

XM * (12 - X)^2 + XM * AX^2

Мы можем вынести из обоих частей XM и упростить выражение:

XM * ((12 - X)^2 + AX^2)

Теперь уравнение может быть записано следующим образом:

XM * ((12 - X)^2 + AX^2) + 12 * XM + 24 * AX + AX^2 * XM = 12 * AX

Дальнейших упрощений или факторизации уравнения не требуется.

Таким образом, для решения данной задачи необходимо вычислить roots уравнения.