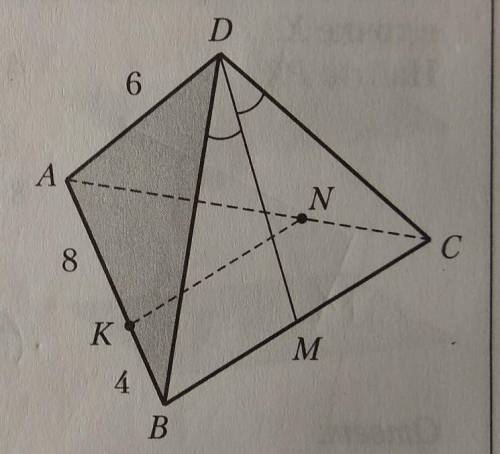
Дано: KN||BC, пл. KNX||DM, где X ∈ AD, AD=6, AK=8, KB=4.
Найти: AX.
Другие вопросы по теме Геометрия
Популярные вопросы
- На малюнку зображено правильну трикутну піраміду SABC. Довжина ребра основи...
3 - Запиши цифрами без пробела и трчки в конце (например, 23), какие по счёту...
1 - Уранение 60. Спишите предложения, подчеркните подле- жаце, определите...
1 - Теңдеуді шеш? 3,2|х|+0,64=13,44...
3 - Чем отличается деятельность людей занятых в производственной сфере деятельности...
3 - Составить эссе на тему язык клад народа...
2 - Найдите лишнее Айбалта Найза Сапы Аударыспак...
3 - 1.Сырбай Мәуленов кім және қайда дүниеге келген? 2.Ақынның алғашқы өлеңдері...
3 - Заполни таблицу, распределив следующие источники по видам: жилище древних...
2 - Як ви розумієте поняття вітаїзм?...
1
Во-первых, если KN || BC, то мы знаем, что углы KNX и KMB - соответственные углы, значит, они равны друг другу: KNX = KMB.
Во-вторых, если KNX || DM, то угол KNX также равен углу D.
Используя информацию из задачи, мы можем составить следующую пропорцию:
AK / KB = AD / DX
Подставляя известные значения, получим:
8 / 4 = 6 / DX
Можем привести пропорцию к виду:
2 = 6 / DX
Умножим обе части пропорции на DX, чтобы избавиться от знаменателя:
2DX = 6
Разделим обе части пропорции на 2, чтобы найти значение DX:
DX = 6 / 2
DX = 3
Теперь у нас есть значение DX, но нам нужно найти AX. Известно, что AX = AD - DX, поэтому мы можем подставить известные значения:
AX = 6 - 3
AX = 3
Таким образом, мы нашли, что AX равно 3.