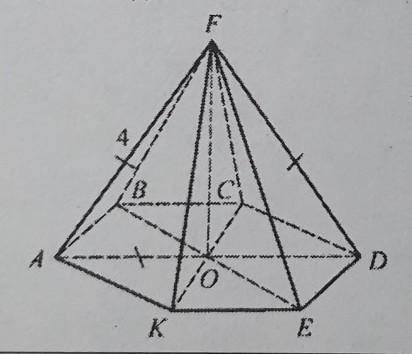
Дано: FABCDEK – правильная пирамида. FO ⊥ (ABC), FM ⊥ АК, AF = 4 Найти: Sосн ​

Для решения данной задачи мы будем использовать сведение ее к более простой геометрической фигуре и применение соответствующих формул.

Дано, что пирамида FABCDEK является правильной пирамидой. Это означает, что ее боковые стороны равны между собой и ее вершина F находится на одинаковом расстоянии от всех боковых сторон.

Дано также, что луч FO перпендикулярен плоскости основания (ABC), луч FM перпендикулярен ребру AK, и что AF = 4.

Мы хотим найти Sосн, то есть площадь основания пирамиды (ABC).

Для начала давайте рассмотрим треугольник ABC. Мы знаем, что луч FO перпендикулярен плоскости этого треугольника, значит, он является высотой треугольника.

Также мы знаем, что AF = 4, что означает, что FO также является высотой треугольника. Теперь у нас есть две высоты треугольника: FO и FM.

Мы можем заметить, что треугольник FOM является прямоугольным треугольником, так как лучи FM и FO перпендикулярны ребрам AK и ABC соответственно.

Теперь мы можем воспользоваться формулой площади прямоугольного треугольника S = (1/2) * a * b, где a и b - это длины катетов треугольника.

Для треугольника FOM длина катета FM равна 4 (так как FM = AF) и длина катета FO равна Sосн. Поэтому мы можем записать формулу для площади треугольника FOM:

Sом = (1/2) * 4 * Sосн = 2 * Sосн

Так как пирамида FABCDEK является правильной, то площадь основания пирамиды равна площади треугольника ABC.

Таким образом, Sосн = Sом / 2.

Итак, мы получаем следующее решение:

1. Найдем Sом, пользуясь формулой площади прямоугольного треугольника: Sом = 2 * Sосн.
2. Найдем Sосн, разделив Sом на 2.

Обратите внимание, что для полного решения нам не хватает информации о длине катета FO или других известных значений. Если вы предоставите дополнительную информацию или формулы, мы сможем дать более точный и подробный ответ.