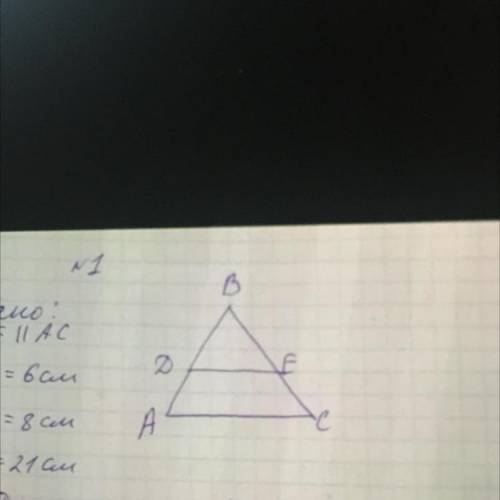
Дано:
DE || (параллельно) AC
AD=6см
BD=8см
AC=21см
1) Доказать,что АВ:ВD=CB:BE
2) Найти DE

Для решения этой задачи, мы можем использовать теорему Талеса и свойства параллельных прямых.

1) Доказательство отношения АВ:ВD=CB:BE:

Воспользуемся теоремой Талеса, которая гласит, что если две прямые AB и CD пересекаются третьей прямой EF параллельно, то отношение длин отрезков, образованных этими прямыми, одинаково.

Итак, у нас дано DE || AC. Если мы проведем прямую DF, то прямые DE и AC также пересекут ее в точках F и G соответственно.

Теперь рассмотрим треугольники ADF и CBG. У этих треугольников соответственные стороны параллельны, поэтому они подобны.

Все это можно записать следующим образом:

1) Отношение сторон треугольников CDF и ABG одинаково:
AB / GD = BG / CF

2) Равенство сторон треугольников CDF и ABG:
AB / GD = CD / DF

3) AB/GD=CD/DF

Теперь посмотрим на треугольник CBD.
У него сторона BD является боковой стороной треугольника CDF, а сторона CD является основанием треугольника CDF.
Поскольку соотношение сторон сохранилось, то мы можем записать:

4) BD/GD = CD/DF

Теперь сравним равенства (3) и (4). Мы видим, что они имеют одинаковые соотношения одного отрезка к другому, поэтому:

AB/GD = BD/GD

Убираем GD с обеих сторон:

AB = BD

Теперь докажем, что CD/DF = BE/GF:

Итак, мы знаем, что треугольники CDF и ABG подобны, поэтому:

CD/DF = BG/CF

Мы также знаем, что треугольники BGD и DGF подобны, поэтому:

BE/GF = BD/DF

Но мы имеем равенство:

BD/DF = CD/DF

Сравниваем равенства (CD/DF) и (BD/DF), получаем:

CD/DF = BE/GF

Из равенств AB = BD и CD/DF = BE/GF следует, что:

AB:BD = CD:BE

Итак, мы доказали, что AB:BD = CD:BE, что и требовалось доказать.

2) Найдем DE:

Используя теорему Пифагора в треугольнике ADE, можем записать:

AD^2 + DE^2 = AE^2

Подставляем известные значения:

6^2 + DE^2 = 21^2

36 + DE^2 = 441

DE^2 = 441 - 36

DE^2 = 405

DE = √405

DE = 3√45

DE ≈ 3 * 6.71

DE ≈ 20.13 см

Таким образом, длина отрезка DE составляет примерно 20.13 см.