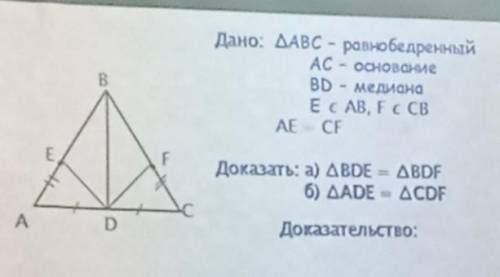
Дано: ДАВС - равнобедренный AC - основание BD - медиана Е с AB, Fc CB AE CF Доказать: а) ABDE - ABDF 6) AADE - ACDF Доказательство:
Другие вопросы по теме Геометрия
Популярные вопросы
- Можно ли школьный этикет считать корпоративным? поясните своё мнение...
3 - Одна из первых стран где появились деньги...
2 - Почему у земноводных 2 круга кровообращения?...
2 - 4. какие отличия строения внутренних органов и поведения птиц характеризуют...
1 - Вставь пропущенные числа: 8471м=..; 5кг 6г=; 500см=; ; 436дм=; 7м3см=....
3 - Хозяйка купила 4 кг 500 г картофеля,кочан капусты весом 3 кг 850 г и моркови.на...
2 - Какие из следующих утверждений верны? а)молекулы состоят из атомов б)атомы...
3 - Велосипедист проехал 23 км за 2 ч.какова скорасть велосипедиста? решения...
3 - Какие общие черты есть у помещиков в поэме гоголя мёртвые души ?...
2 - Напишите сочинение-рассуждение,раскрывая смысл высказывания а.п.чехова:...
1
а) Докажем, что треугольники ABDE и ABDF равны.
1. Из условия дано, что треугольник DAVS равнобедренный, поэтому у него сторона DA равна стороне SA.
2. Также дано, что BD - медиана, поэтому медиана BC делит сторону DA пополам, то есть сторона DA равна стороне AD.
3. Значит, сторона AD равна стороне SA, тогда треугольник ASD равносторонний.
4. Так как у треугольника ASD все стороны равны, то его углы также равны 60 градусов.
5. Поскольку угол BAD является смежным углом углу DAS и углу ASD, то он также равен 60 градусов.
6. У треугольника ABF гипотенуза AF равна стороне SA (так как у треугольника ASD все стороны равны), а угол ABF равен углу BAD (поэтому он тоже равен 60 градусов).
7. Таким образом, у треугольников ABDE и ABDF равны две стороны и один угол (все равны 60 градусов), что означает их равенство.
б) Докажем, что треугольники AADE и ACDF равны.
1. Заметим, что треугольники AADE и ACDF являются прямоугольными треугольниками со значением прямого угла.
2. У треугольника AADE у нас есть два равных угла, так как они являются вертикальными углами (угол BAD равен углу AED поэтому их и считаем равными).
3. Также у треугольника ACDF также есть два равных угла - угол ACD равен углу DCF поэтому их и считаем равными.
4. Значит, треугольники AADE и ACDF имеют два равных угла, что говорит о их равенстве.
Таким образом, мы доказали, что треугольники ABDE и ABDF равны, а также треугольники AADE и ACDF равны.