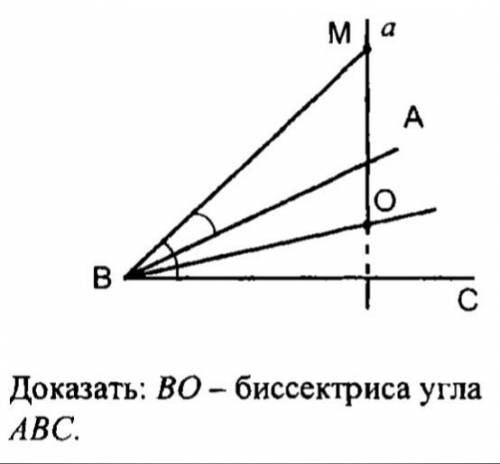
Дано, что прямая α⊥ плоскости АВС.
Доказать, что ВО - биссектриса угла АВС.
Другие вопросы по теме Геометрия
Популярные вопросы
- Аналіз верша позні шыпшыннік...
3 - 1. Місце, де жив лось до заповідника. 3. Що пообіцяв дядько віддати...
2 - У6 класі 25 учнів,причому хлопців у 4 разименше, ніж дівчат.Скільки...
2 - Iз точки О, яка належить бісектрисі ВМ трикутника АВС, проведено...
1 - Сумма противоположных сторон вписанного четырехугольника 39 см...
3 - Какие виды ионизирующих излучений проходят через атмосферу с наименьшим...
2 - Мәңгілік ел құндылықтарыМәндес сөзді тап.Алпауыттатукеңзор...
3 - Провідміняйте числівник 537...
1 - Уривок про характер Митька з твору митькозавр з юрківки...
1 - Контрольний пересказ тексту наукового стилю (із використанням...
1
Давайте начнем с определений. Биссектриса угла - это линия, которая делит данный угол на две равные части. Для этого линия должна проходить через вершину угла и разделить его на две равные части на противоположных сторонах.
На данной диаграмме у нас есть прямая α, которая перпендикулярна к плоскости АВС. Мы должны доказать, что ВО - биссектриса угла АВС.
Для начала обратим внимание на стороны угла АВС. У нас есть сторона АВ, сторона АС и сторона ВС. В данном случае, стороны АВ и АС являются лучами угла, а сторона ВС - это отрезок, соединяющий концы лучей угла.
Теперь обратим внимание на точку О. Она находится на прямой α и расположена между вершиной угла АВС и стороной ВС. Заметим, что линия ВО проходит через вершину угла и делит его на две части - угол АВО и угол ОВС.
Чтобы доказать, что линия ВО - биссектриса угла АВС, нам нужно показать, что угол АВО равен углу ОВС.
Воспользуемся свойством перпендикулярных прямых. По определению прямая α перпендикулярна к плоскости АВС, что означает, что она проходит через центр ее пересечения.
Теперь представим, что центр пересечения плоскости АВС находится в точке О. Поскольку прямая α проходит через эту точку, угол АВО и угол ОВС образуются между прямой α и стороной ВС, и поэтому они должны быть равными.
Таким образом, мы доказали, что ВО - биссектриса угла АВС.
Важно отметить, что данное доказательство предполагает, что прямая α действительно перпендикулярна к плоскости АВС и пересекает ее в точке О. Если эти предпосылки не выполняются, то доказательство не будет считаться правильным.
Если у тебя остались какие-либо вопросы, не стесняйся задавать их!