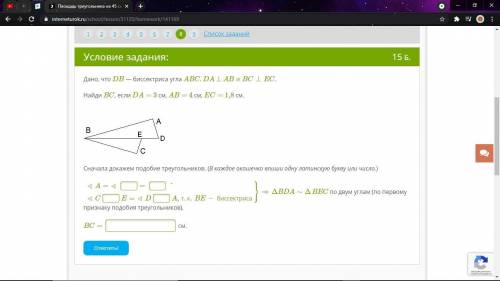
Дано, что DB — биссектриса угла ABC. DA⊥ABиBC⊥EC. Найди BC, если DA= 3 см, AB= 4 см, EC= 1,8 см.
Сначала докажем подобие треугольников. (В каждое окошечко впиши одну латинскую букву или число.)
∢A=∢
=
°∢C
E=∢D
A,т.к.BE− биссектриса}⇒ΔBDA∼ΔBEC по двум углам (по первому признаку подобия треугольников).
BC=
см..
Другие вопросы по теме Геометрия
Популярные вопросы
- Написать сочинение. нужно уже на четверг 19 числа. утром надо уже...
2 - Сильные черты ярослава мудрого,и почему именно они?...
2 - 1.с каких операций можно обрезать часть аудиозаписи? 2.какие операции...
2 - Correct the mistakes in the sentences. 1. peter asked that if i knew...
1 - Особенности сказок народов мира...
3 - Записать два двузначных числа, у которых в рязряде десятков записана...
2 - 6глаголов 1 и 2 спряжения в ед числе...
3 - Можете написать сочинение на тему почему вася подружился с марусей...
1 - Масса 1 м^3 повітря при н.у 1.293 кг. яка масса цьго ж об єму повітря...
2 - Поступки и действия героя в эпизоде теплый хлеб...
1
Дано, что DB — биссектриса угла ABC. Значит, мы можем сделать следующий вывод:
∢A = ∢C (соответствующие углы при биссектрисе равны)
Также дано, что DA ⊥ AB и BC ⊥ EC. Это означает, что углы D и E являются прямыми углами.
Теперь мы можем приступить к доказательству подобия треугольников ΔBDA и ΔBEC.
По теореме о двух углах мы знаем, что если два угла одного треугольника равны двум углам другого треугольника, то эти треугольники подобны.
Таким образом, мы можем сделать вывод о подобии треугольников ΔBDA и ΔBEC по первому признаку подобия треугольников (угл-угл).
Теперь, используя понятие подобия треугольников, можем установить соотношение между сторонами треугольников ΔBDA и ΔBEC.
Основываясь на подобии треугольников ΔBDA и ΔBEC, мы можем установить следующее соотношение:
BD/BE = DA/EC
Заменяем известными значениями:
BD/BE = 3/1.8
Далее, чтобы найти длину отрезка BC, нам нужно знать значение BD.
Однако, нам даны значения только для сторон треугольника ΔBDA.
Решим данную проблему, используя теорему Пифагора для прямоугольного треугольника ΔBDA:
BD^2 = AB^2 - DA^2
Заменяем значениями:
BD^2 = 4^2 - 3^2
BD^2 = 16 - 9
BD^2 = 7
BD = √7
Теперь, зная значение BD, мы можем найти значение BC.
Используем ранее установленное соотношение:
BD/BE = 3/1.8
Подставляем значения:
√7/BE = 3/1.8
Умножаем обе части равенства на BE:
√7 = (3/1.8)*BE
Делим обе части равенства на (3/1.8):
√7/(3/1.8) = BE
Упрощаем:
√7 * (1.8/3) = BE
Вычисляем:
√7 * 0.6 ≈ 0.7745 ≈ BE
Теперь мы можем найти значение BC.
По теореме Пифагора применим к треугольнику ΔBEC:
BC^2 = BE^2 + EC^2
Заменяем значениями:
BC^2 = 0.7745^2 + 1.8^2
BC^2 = 0.6001 + 3.24
BC^2 ≈ 3.8401
BC ≈ √3.8401
BC ≈ 1.96
Таким образом, длина отрезка BC примерно равна 1.96 см.