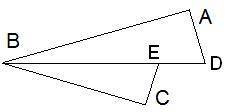
Дано, что BE — биссектриса угла ABC. AD⊥ABиCE⊥CB.
Найди EB, если AD= 12 см, AB= 16 см, CE= 8,4 см.

Сначала докажи подобие треугольников.

EB=
см.

Для начала, мы должны доказать подобие треугольников. Подобие треугольников можно доказать, если у них соответствующие углы равны, а соответствующие стороны пропорциональны.

У нас есть два треугольника: треугольник ABD и треугольник CBE. Мы знаем, что угол BAD и угол EBC равны, так как они оба прямые углы соответственных треугольников.

Теперь мы должны доказать, что соответствующие стороны пропорциональны. Для этого мы можем использовать теорему биссектрисы.

Теорема биссектрисы гласит, что в треугольнике биссектриса делит противоположную сторону в пропорции длин двух других сторон. Из этой теоремы следует, что отношение длин сторон AB и AD будет равно отношению длин сторон BC и CE, так как BE является биссектрисой угла ABC.

Давайте это проверим. Мы знаем, что AD= 12 см и AB= 16 см. Таким образом, отношение длин сторон AB и AD равно 16/12 = 4/3.

Теперь найдем отношение длин сторон BC и CE. Мы знаем, что CE= 8,4 см, поэтому отношение длин сторон BC и CE равно BC/8,4.
Пусть EB=x см, тогда BC=x+8.4 см.

Теперь мы можем записать пропорцию:
(BC)/(CE) = (AB)/(AD)
(x+8,4)/8,4 = 16/12

Для решения этого уравнения мы можем умножить обе стороны на 8,4, чтобы избавиться от знаменателя:
x + 8,4 = 8,4 * (16/12)

Упростим правую часть:
x + 8,4 = 11,2

Теперь вычтем 8,4 из обеих сторон уравнения:
x = 11,2 - 8,4

x = 2,8

Таким образом, EB = 2,8 см.

Таким образом, длина стороны EB равна 2,8 см.