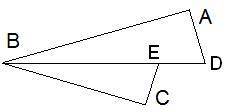
Дано, что BD — биссектриса угла ABC. DA⊥BA и CB⊥EC. Вычисли EB, если DA= 15 см, BA= 20 см, EC= 3 см.
Сначала докажи подобие треугольников.
(В каждое окошечко пиши одну букву или число.)
∢A=∢__=__°
∢C__D=∢DBA,т.к. __ E− биссектриса}⇒ΔDBA∼ΔEBC, по двум углам (по первому признаку подобия треугольников).
EB= __см.
Другие вопросы по теме Геометрия
Популярные вопросы
- Сколько натуральных решений неравенства 3с -2,7 принадлежит промежутку [0;...
1 - 1) Euclid stated, ‘The three angles of a triangle are equal to two right angles”...
3 - работу надо успеть сдать до работу надо успеть сдать до работу надо успеть...
2 - Визначити період піврозпаду радіоактивного елемента, якщо через інтервал часу...
3 - Проверочная работа по теме «Галактики» Вариант 1 Млечный Путь - это: 1) туманность...
1 - Определите электроёмкость С1 конденсатора, если ёмкость батареи, изображённой...
1 - Стереометрия (геометрия Стереометрия (геометрия...
3 - Ребят контрольная идёт Составьте уравнения реакций, назовите продукты реакций:...
1 - Объясните тему: химические уравнения с примерами)...
2 - Установіть відповідність між рівняннями та їх коренямих + 2 = 1 - 4х безліч...
1
Угол ADB является прямым, так как DA ⊥ BA. Угол BAC и угол CAB являются смежными и, следовательно, равными. Так как BD является биссектрисой угла ABC, то угол CBD также равен углу ABD.
Таким образом, у нас есть две пары равных углов: угол DBA равен углу EBC, и угол ABD равен углу CBD.
Следовательно, треугольники ΔDBA и ΔEBC подобны по первому признаку подобия треугольников (УУ).
Теперь, чтобы найти значение EB, нам нужен коэффициент подобия между этими треугольниками.
Мы можем использовать соотношение сторон, чтобы найти коэффициент подобия:
EB / BA = EC / DA
Подставляя известные значения, получим:
EB / 20 = 3 / 15
Упростим это соотношение:
EB / 20 = 1 / 5
Перемножим обе стороны на 20, чтобы избавиться от знаменателя:
EB = 20 * (1 / 5)
EB = 4 см
Таким образом, EB равно 4 см.