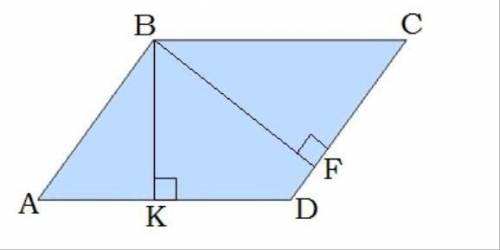
Дано: CD=5 см, AD=7 см, BК=3 см. Найти: S ABCD.​
И если вам не сложно, то перейдите на мой предыдущий вопрос и решите его

4 * 9 = 36 (умножаем высоту на основание)

ВК * AD

Объяснение:

Удачи

Добрый день! Для решения этой задачи, мы можем воспользоваться формулой площади прямоугольника, которая гласит: "Площадь прямоугольника равна произведению длины одной из его сторон на длину другой стороны".

Сначала нам необходимо определить, какие стороны прямоугольника ABCD здесь являются основаниями, а какие являются высотами. Для этого, давайте разберемся с обозначениями.

В задаче даны отрезки CD, AD и BK. Отрезки BK и CD соприкасаются, поэтому они являются сторонами прямоугольника.
Отрезок AD является высотой прямоугольника, так как он перпендикулярен к основанию и проходит через одну из его вершин.

Теперь, когда мы определили основания и высоту, мы можем использовать формулу площади прямоугольника.

S_ABCD = CD * AD

Для нашей задачи, нам известны значения этих сторон. Вместо CD подставляем 5 см, так как это значение дано в условии.
Вместо AD подставляем 7 см, так как и это значение также дано в условии.

S_ABCD = 5 * 7
S_ABCD = 35 (см^2)

Таким образом, площадь прямоугольника ABCD равна 35 см^2.