Дано:
BA=20М
OA=25М
Найти
AC=
OC=

АС-20м ОС-12,5м

Объяснение:

всё просто

Для решения этой задачи воспользуемся теоремой Пифагора и синусами.

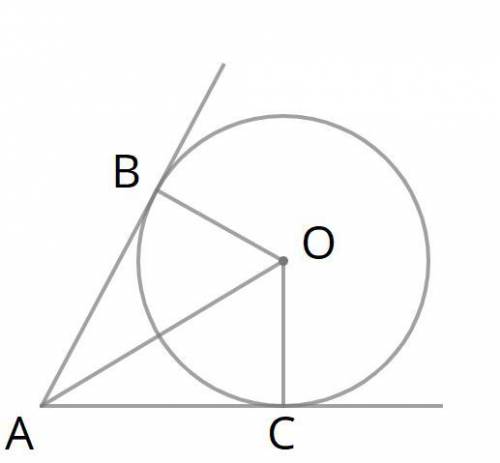
1. Найдем длину отрезка AC.
Из данной картинки видно, что треугольник BAC - прямоугольный. Мы знаем, что BA = 20 метров, OA = 25 метров. Согласно теореме Пифагора, для прямоугольного треугольника квадрат длины гипотенузы равен сумме квадратов длин катетов.
Таким образом, мы можем записать уравнение:
BA^2 + AC^2 = OA^2,
20^2 + AC^2 = 25^2,
400 + AC^2 = 625,
AC^2 = 625 - 400,
AC^2 = 225,
AC = √225,
AC = 15 метров.

Ответ: AC = 15 метров.

2. Найдем длину отрезка OC.
Так как OC - это катет прямоугольного треугольника BOC, мы можем использовать теорему Пифагора еще раз:
OC^2 = BC^2 + OB^2.
Мы имеем информацию о длинах OB и BC?
OB = OA - BA = 25 - 20 = 5 метров.
BC = BA - AC = 20 - 15 = 5 метров.
Теперь мы можем подставить значения в уравнение:
OC^2 = 5^2 + 5^2,
OC^2 = 25 + 25,
OC^2 = 50,
OC = √50,
OC = 5√2 метров.

Ответ: OC = 5√2 метров.