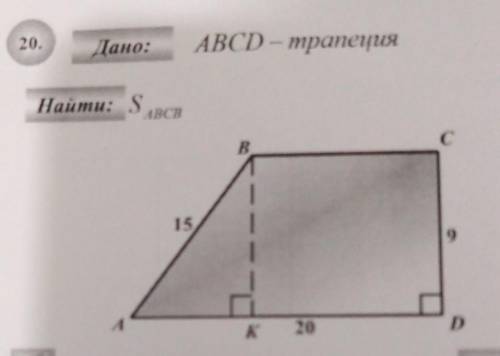
Дано: АВСD – прямоугольная трапеция, AB=15, KD=20, CD=9, угол CDK=90°, угол AKB=90°
Найти: Площадь трапеции
Другие вопросы по теме Геометрия
Популярные вопросы
- 1. сформулируйте следствия вращения земли а) вокруг своей оси б) вокруг...
2 - Назовите известные виды опер эпохи барокко...
3 - За 2 кг рыбы и 1 кг мяса заплатили 134 грн. сколько стоит 1кг рыбы и 1кг...
3 - Квадратные уровнения x(в квадрате)-7x+12=0...
2 - Биологи, подключаемся, и бедному школьнику, который не шарит в биологии....
1 - Задали сочинение анатолий погорельский (черная курица, или подземные жители)...
2 - Володя прополол 9 грядок катя на 3 грядки больше а ира на 18 грядок меньше...
3 - Вкаком ряду в обоих словах пропущена одна и та же буква? 1) дремл..щий,...
3 - 40 люди, , надо мне нужна характеристика главных героев из произведения...
3 - Согласные звуки которые всегда находятся в сильной позиции...
3
Шаг 1: Найдем высоту трапеции h.
Обратим внимание на прямоугольные треугольники CDK и AKB. Они имеют по одному прямому углу и смежные углы AKB и CDK.
Таким образом, треугольники CDK и AKB подобны друг другу по критерию "угол-прямоугольник-угол", или УПУ.
Шаг 2: Используя свойство подобных треугольников, найдем высоту h.
Отношение соответствующих сторон пропорциональных треугольников равно. Поэтому,
AB / AK = CD / CK
Подставим известные значения:
15 / AK = 9 / CK
Чтобы решить эту пропорцию, воспользуемся теоремой Пифагора для каждого из треугольников:
AK^2 + CK^2 = AB^2
Для треугольника AKB:
AK^2 + h^2 = 15^2
Для треугольника CDK:
CK^2 + h^2 = CD^2 = 9^2
Подставим значения:
AK^2 + h^2 = 225 (Уравнение 1)
CK^2 + h^2 = 81 (Уравнение 2)
Вычтем Уравнение 2 из Уравнение 1, чтобы убрать переменную h:
AK^2 - CK^2 = 225 - 81
(AK + CK)(AK - CK) = 144
Шаг 3: Найдем AK и CK.
Заметим, что AK = AB + BK и CK = CD - DK, поэтому:
AK = 15 + BK
CK = 9 - 20
Подставим значения обратно в Уравнение 1:
(15 + BK + 9 - 20)(15 + BK - 9 + 20) = 144
(4 + BK)(36 + BK) = 144
Раскроем скобки:
144 + 4BK + 36BK + BK^2 = 144
BK^2 + 40BK = 0
BK(BK + 40) = 0
BK = 0 или BK = -40
Примем BK = 0 (поскольку отрицательное значение не имеет смысла в данном контексте).
Таким образом, AK = 15 + 0 = 15 и CK = 9 - 20 = -11.
Теперь подставим AK и CK в Уравнение 1:
AK^2 + h^2 = 225
15^2 + h^2 = 225
h^2 = 225 - 225
h^2 = 0
Следовательно, h = 0.
Шаг 4: Найдем площадь трапеции.
Трапеция может рассматриваться как сумма двух прямоугольных треугольников ABK и CDK, или как сумма площадей прямоугольника ACDK и прямоугольного треугольника BC.
Площадь прямоугольника ACDK равна CD * AK:
9 * 15 = 135
Площадь прямоугольного треугольника BC равна (1/2) * CK * h:
(1/2) * (-11) * 0 = 0
Таким образом, площадь трапеции равна 135 + 0 = 135.