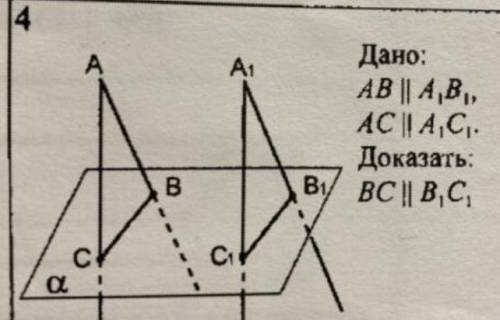
Дано: АВ параллельна А1В1 АС параллельна А1С1. Доказать: ВС параллельна В1С1

Дано, что AB || A1B1 и AC || A1C1. Требуется доказать, что BC || B1C1.

Чтобы доказать данное утверждение, мы воспользуемся свойством параллельных прямых.

Согласно этому свойству, если две прямые AB и CD пересекаются третьей прямой EF, и эти прямые параллельны друг другу, то соответствующие углы равны между собой.

Обозначим точку пересечения прямых AB и A1B1 как D, а точку пересечения прямых AC и A1C1 как E.

Так как AB || A1B1 и AC || A1C1, угол BDA равен углу B1DA1 и угол EDA равен углу E1DA1.

Теперь рассмотрим треугольник BDC и треугольник B1D1C1. У них две пары равных углов: BDA равен B1DA1 и угол BCD равен углу B1C1D1.

Так как у этих треугольников две пары равных углов, то треугольники подобны.

Так как два треугольника подобны, то соответствующие стороны пропорциональны.

Следовательно, мы можем записать следующее соотношение:

BD/BD1 = BC/BC1

Отсюда получаем, что BC || B1C1, так как соотношение между сторонами построенных треугольников говорит нам о параллельности сторон BC и B1C1.

Таким образом, доказано, что ВС параллельна В1С1.