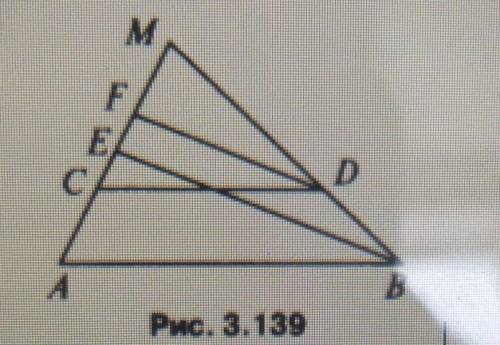
Дано: АВ||CD, BE биссектриса угла DBA, DF биссектриса угла CDM. Пересекаются ли прямые DF и BE?

Чтобы определить, пересекаются ли прямые DF и BE, нам нужно рассмотреть данные и применить соответствующие геометрические свойства и правила.

Дано, что AB || CD. Это означает, что отрезки AB и CD параллельны и не пересекаются нигде. Параллельные прямые имеют одинаковый наклон, поэтому углы АВE и CDЕ равны (как вертикальные углы). Таким образом, у нас есть первое свойство:

1. Углы АВE и CDЕ равны.

Далее, нам известно, что BE является биссектрисой угла DBA, а DF - биссектрисой угла CDM. Биссектриса угла делит его на два равных угла. Это означает, что углы DBE и ABE равны, а также углы CDF и FDM равны. Кроме того, сумма углов DBE и ABE должна быть равна 180 градусов, так как они являются смежными углами в линейной паре. То же самое верно и для углов CDF и FDM. Получаем второе свойство:

2. Углы DBE и ABE равны; углы CDF и FDM равны; суммы углов DBE и ABE, а также CDF и FDM равны 180 градусов.

Наша задача - проверить, пересекаются ли прямые DF и BE. Если они пересекаются, значит, существует точка пересечения, обозначим ее как P. Если же они не пересекаются, то значит, прямые параллельны, и у нас не будет точки пересечения.

Предположим, что прямые DF и BE пересекаются в точке P.

Тогда, у нас есть следующие углы:
- Углы DPF и EPB (вертикальные углы)
- Углы FDM и MDE (вертикальные углы)
- Углы CDF и FDC (углы в общем соответствующем положении)

Углы DPF и EPB равны по построению (описание задачи), так как они являются вертикальными. Также, углы FDM и MDE равны по построению, так как они тоже являются вертикальными.

Но углы CDF и FDC не могут быть одновременно равными углам DPF и EPB, потому что:
CDF + FDC = 180 градусов (по свойству 2)
DPF + EPB = 180 градусов (вершина FDPB является прямым углом)
CDF + FDC ≠ DPF + EPB, так как CDF и FDC не равны DPF и EPB (свойство 1)

Из этого можно сделать вывод, что прямые DF и BE не пересекаются.

Таким образом, ответ на вопрос: прямые DF и BE не пересекаются.