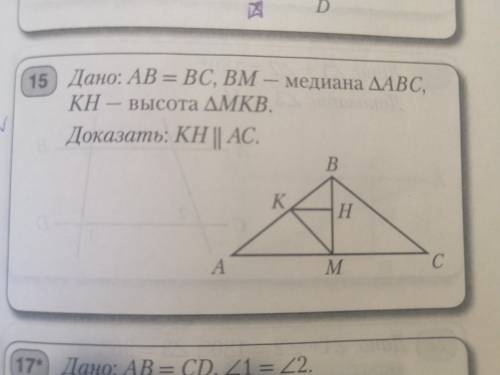
Дано: АВ=BC, BM-медиана тр. ABC, KH-высота тр. MKB
Доказать: KH||AC

Объяснение:

ВМ - медиана равнобедренного ΔАВС ( т.к АВ=ВС) является биссектрисой и высотой ⇒ВМ ⊥ АС

КН - высота ΔМКВ ⇒ КН ⊥ ВМ

прямая АС и КН перпендикулярны одной прямой ВМ ,

следовательно они параллельны АС ║ KH , что и требовалось доказать

Объяснение:

1) ВМ- медиана и высота (ΔАВС - равнобедренный (АВ=ВС))

2) КН║АС ( секущая ВМ перпендикулярна к прямой, содержащей отрезок КН, и перпендикулярна к прямой, содержащей отрезок АС) по теореме о параллельности прямых (если параллельные прямые пересечены секущей, то накрест лежащие углы равны), так как ∠МНК=90° и ∠ВАМ= 90°, то ∠МНК=∠ВАМ.

1) КН║АС ( ВМ⊥КН и ВМ⊥АС) по следствию ( если две прямые перпендикулярны третьей прямой, то они параллельны) теоремы о параллельности прямых (если параллельные прямые пересечены секущей, то накрест лежащие углы равны)