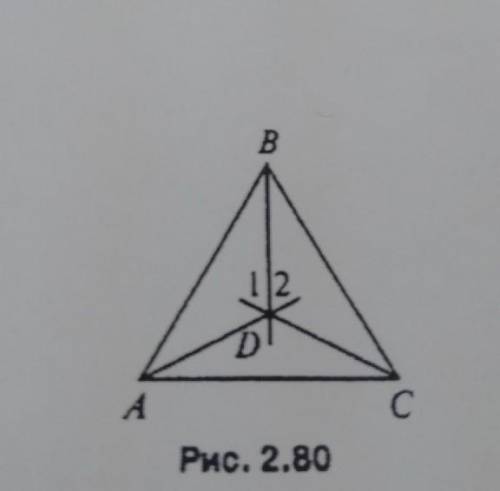
Дано adc равнобедренный угол 1=угол 2 доказать abc равнобедренный

Для доказательства того, что треугольник ABC является равнобедренным, нам необходимо использовать информацию о равнобедренном треугольнике ADC, а именно равенство его углов.

Исходя из условия, у нас есть равнобедренный треугольник ADC, в котором угол 1 равен углу 2.

Для начала, давайте обозначим точку пересечения высоты из вершины D с основанием BC как точку H.

При рассмотрении треугольника ADC, мы знаем, что угол 3 является углом прямоугольного треугольника HDC, а угол 4 является углом прямоугольного треугольника EDB. Они равны 90 градусам, так как перпендикулярные линии создают прямой угол.

Известно также, что угол 1 равен углу 3, поскольку треугольник ADC является равнобедренным. Поэтому угол 3 также равен углу 2.

Таким образом, мы имеем: угол 3 = углу 1 = углу 2.

Теперь рассмотрим треугольник ABC. По построению, угол 3 является внутренним углом треугольника ABC, поскольку хорда BC проходит через него.

Зная, что угол 3 равен углу 2, мы можем сделать вывод, что угол 2 также является внутренним углом треугольника ABC.

Следовательно, у нас есть два внутренних угла треугольника ABC, которые равны друг другу: угол 2 и угол 4.

Аналогичным образом, мы можем также установить, что уголы 1 и 4 также равны друг другу.

Таким образом, у нас есть две пары равных углов: углы 1 и 4, а также углы 2 и 3.

По определению равнобедренного треугольника, равенство двух пар углов означает, что соответствующие им стороны равны.

Из конструкции треугольника ABC мы видим, что сторона AB является основанием и равна стороне AC.

Таким образом, мы можем заключить, что треугольник ABC является равнобедренным, поскольку его две боковые стороны, AB и AC, равны друг другу.

Таким образом, теорема о равнобедренном треугольнике доказана.