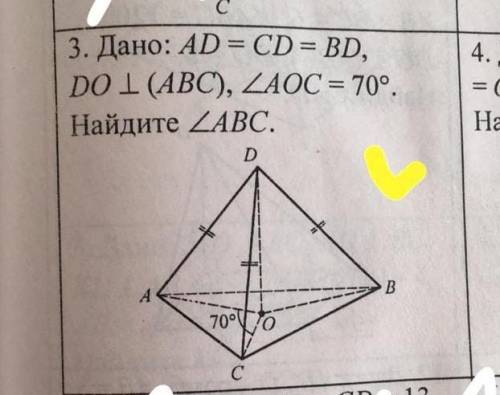
Дано: АД=СД=ВД.. Остальное на фото↑
Ребята, кому не трудно
Другие вопросы по теме Геометрия
Популярные вопросы
- За 7 дней 5 львов 175 кг мяса ск.мяса сьест один лев за сутки...
1 - 3класс придумать сказку 8 предложений. (для девочки)...
2 - X+2y+z=-1 3x-2y+z=-1 -2x+2y+3z=5 решить систему методом крамера...
1 - Кто изображён в этом описании? родом из города, который теперь считается...
2 - ответьте на вопросы: 1 что вы понимаете под объектом и предметом педагогической...
3 - Определите расстояние от: экватора до полюса, от москвы до аддис-абеба,...
2 - Средние века. на чём основывалась независимость крупных феодалов по отношению...
3 - Контрольный диктант шел васютка по тайге, следил за памятками на деревьях...
2 - Камень дерево кость по какому принцу образованы ряды...
3 - 1) 2x-3=5-2x 2) 2x-1/3 + x+1/2=2 уравнение с одной переменной. ! заранее...
3
Задача на описанную окружность .
Объяснение:
Тк.DO⊥(ABC) , то ∠DOA=∠DOB=∠DOC=90°. Тогда прямоугольные треугольники ΔDOA=ΔDOB=DOC равны катету и гипотенузу ⇒ОА=ОВ=ОС ⇒О-центр описанной окружности около ΔАВС.
Тогда ∠АОС=70° центральный⇒ дуга ∪АС=70° . Угол ∠АВС -вписанный и опирается на ту же дугу ∠АВС=1/2*70=34°