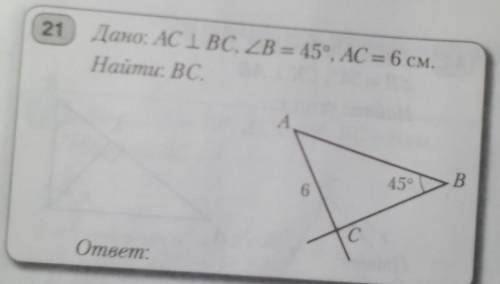
Дано: AC перпендикулярно BC угол B = 45° AC = 6 см найти BC​

Ювадададдададпзп

Объяснение:

Сорри надо балы(

Для решения данной задачи нам понадобится знание о свойствах перпендикуляра и применение тригонометрических функций.

Сначала обратимся к свойствам перпендикуляра. Перпендикуляр - это прямая, которая образует прямой угол с другой прямой. В данной задаче мы имеем, что прямая AC перпендикулярна прямой BC.

Рассмотрим треугольник ABC. Угол B равен 45° и прямая AC перпендикулярна прямой BC. Мы хотим найти длину отрезка BC.

Для начала, давайте определимся, какие известные данные у нас есть. У нас дано, что AC = 6 см.

Далее, мы можем использовать тригонометрическую функцию тангенс для нахождения значения отношения длины противолежащего катета к длине прилежащего катета.

В данной задаче можно воспользоваться тангенсом угла B. Тангенс угла B равен отношению противолежащего катета (BC) к прилежащему катету (AC).

Таким образом, мы получаем уравнение:

tan(B) = BC/AC

Подставляя известные значения, получаем:

tan(45°) = BC / 6

Так как тангенс 45° равен 1, заменим его соответствующим значением:

1 = BC / 6

Для того чтобы найти BC, мы можем перемножить обе стороны уравнения на 6:

1 * 6 = BC

6 = BC

То есть, BC равно 6 см.

Таким образом, мы нашли, что длина отрезка BC равна 6 см.