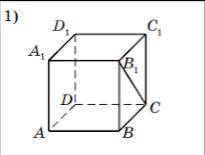
Дано: ABCDA1B1C1D1 - куб. Докажите, что B1C⟂ (перпендикулярно) DC.

Для начала, давайте вспомним определения и свойства, связанные с кубами.

1. Куб - это особый вид параллелепипеда, у которого все ребра имеют одинаковую длину, а все грани являются квадратами.

2. Зная, что мы имеем дело с кубом ABCDA1B1C1D1, мы можем сделать вывод, что его стороны равны по длине друг другу. Давайте обозначим эту длину за "a".

Теперь рассмотрим треугольники B1C1D1 и DCB1.

Заметим, что сторона B1C1 куба - это диагональ грани B1A1C1, а сторона DC - это ребро куба.

Также, сторона B1D1 куба - это ребро куба, а сторона CB1 - это диагональ грани ACB1.

Требуется доказать, что треугольники B1C1D1 и DCB1 перпендикулярны, то есть угол между ними равен 90 градусов.

Для доказательства, воспользуемся свойством перпендикулярных линий - произведение длин отрезков, образованных перпендикулярными линиями исходит из одной точки, равно другому произведению отрезков, образованных этими перпендикулярными линиями, исходящих из другой точки.

Мы должны доказать, что AB1² + B1C1² = AC² + C1D1² (равенство 1)

Знаем, что сторона AB1 в нашем кубе имеет длину a√2 (так как это диагональ грани ABCD), и стороны B1C1 и AC имеют длину a (как сторона куба).

Тогда левая часть равенства будет: (a√2)² + a² = 2a² + a² = 3a².

Также известно, что сторона C1D1 в нашем кубе равна a (как сторона куба), и сторона DC равна a.

Тогда правая часть равенства будет: a² + a² = 2a².

Таким образом, равенство 1 выполняется: 3a² = 2a².

Из равенства 1 следует, что треугольники B1C1D1 и DCB1 являются перпендикулярными, так как их стороны удовлетворяют свойству перпендикулярных линий.

Таким образом, мы доказали, что B1C1 перпендикулярна DC в кубе ABCDA1B1C1D1.