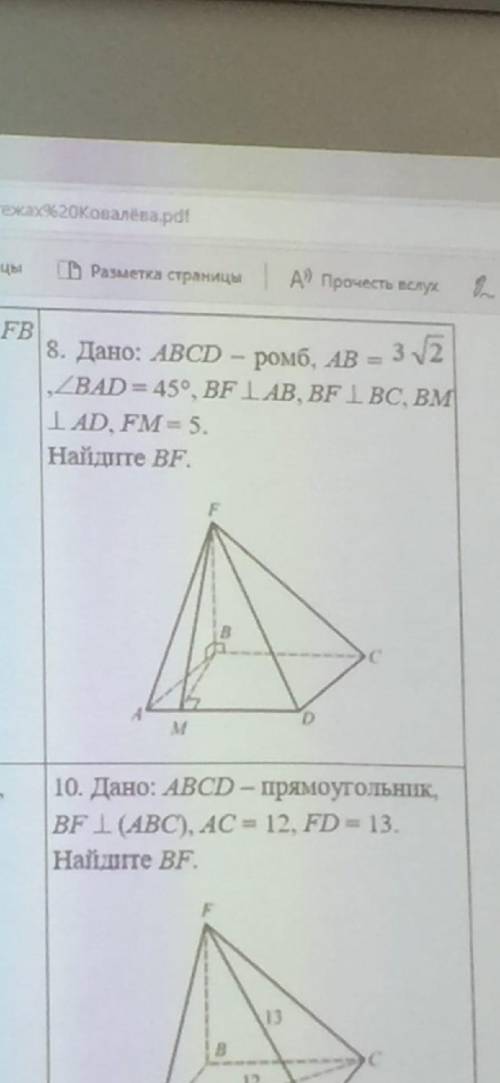
Дано: ABCD - ромб, AB = 3√2, ∠BAD = 45, BF⊥ AB, BF ⊥ BC, BM ⊥ AD, FM = 5. Найти BF
Другие вопросы по теме Геометрия
Популярные вопросы
- Сколько молекул серной кислоты( н2so4) содержится в 980 г?...
2 - Какое время имеет следующее предложение? drawings of a concept idea have...
3 - Снегирей,лесной,северной транскрипция...
1 - Примеры влияния неблагоприятных условий на живые организмы.запишите их...
3 - 40 омонимы: существительное, прилагательное, глагол (примеры)...
3 - Скакой целью проводятся аварийно и другие неотложные работы ( ас днр)...
1 - Pascal abc составить программу. с клавиатуры вводится 3 числа. найти...
3 - Одинаковые традиции в швеции и иране?...
3 - 10 корень квадрата 18 дилить на корень квадрата 2 - корен квадрата 5...
1 - Рассказ о жанне д арк. по плану 1) кто такая жанна.,2)встреча с комендантом,...
2
1. Заметим, что по свойствам ромба, все стороны равны друг другу. Таким образом, AB = BC = CD = DA = 3√2.
2. Также, по определению ромба, у него все углы равны между собой. Таким образом, ∠BCD = ∠CDA = 180 - ∠BAD = 180 - 45 = 135 градусов.
3. Посмотрим на треугольник ABC. У него две перпендикулярные стороны: AB и BF. Так как треугольник прямоугольный, мы можем использовать теорему Пифагора для нахождения стороны BF:
BF^2 = AB^2 - AF^2
По условию, AB = 3√2. Мы знаем, что AF = FM + AM. Из условия, FM = 5. Осталось найти AM.
4. Рассмотрим треугольник BMA. Так как BM ⊥ AD, а ромб ABCD является прямоугольником, угол BMA также равен 90 градусов. Таким образом, у нас есть прямоугольный треугольник с гипотенузой AM и катетами BM и AB.
5. Мы знаем, что AB = 3√2 и BM = AM / 2. Таким образом, BM = AM / 2 = AB / 2 = (3√2) / 2.
6. Вернемся к треугольнику ABC и используем теорему Пифагора:
BF^2 = (3√2)^2 - (FM + AM)^2 = 18 - (5 + AM)^2
7. Для того чтобы продолжить решение, нам нужно найти AM. Для этого рассмотрим треугольник ABM. У него угол B равен 45 градусов, и мы можем применить тригонометрический синус:
sin(B) = BM / AM
sin(45) = (3√2) / AM
AM = (3√2) / sin(45) = 3√2 / (1/√2) = 3√2 * √2 = 3 * 2 = 6.
8. Теперь мы можем вернуться к шагу 6 и продолжить вычисления:
BF^2 = 18 - (5 + 6)^2 = 18 - 11^2 = 18 - 121 = -103
9. Мы получили отрицательное число в квадрате, что не имеет смысла. Это означает, что треугольник не существует и, следовательно, ответ на задачу не существует.
Таким образом, ответ на вопрос "Найти BF" в данной задаче не существует.