1. Геометрия
  2. Дано: abcd параллелограмм,

Дано: abcd параллелограмм, угол а=30, ав=10, вк - высота, опущенная на dc, вк=4 найти: ad, dk, sabcd

Wely Wely    3   09.06.2019 02:20    40

Ответы
shmilkovas shmilkovas  07.07.2020 23:49
Так как угол A-30 градусов, то угол  C тоже равен 30 гр. Рассмотрим треугольник BKC: BC - гипотенуза, BK - катет, лежащий против угла в 30 гр. и равный половине гипотенузы, то есть BC=8, площадь параллелограмма = произведение основания на высоту = 4*10=40. BC=AD=8, с DK посложнее. 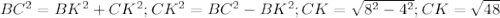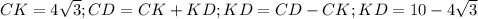Тут надо по теореме Пифагора в том же треугольнике: BC^{2} = BK^{2} + CK^{2}; CK^{2}= BC^{2}-BK^{2}; CK= \sqrt{ 8^{2}- 4^{2} }; CK= \sqrt{48} CK= 4\sqrt{3}; CD=CK+KD; KD=CD-CK; KD=10- 4\sqrt{3}
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
nlogvinova14 nlogvinova14  11.08.2019 13:30
Найдите смежные углы,если один из них в 2,5 раза меньше прямого. уравнением,если можно,....
Мейси13 Мейси13  16.06.2019 23:10
Треугольники abc и kpm равны.kp 2 см рм 4 см км 5 см .найдите периметр треугольника авс...
pmangaskin pmangaskin  16.06.2019 23:10
Abcd-параллелограмм, 0-точка пересечения диагоналей. м- середина ав, da(вектор)=а (вектор). dc( вектор) =b (вектор). выразите через векторы а и b следующие векторы: a)...
Dasha2006rrtt Dasha2006rrtt  02.08.2019 09:50
Вчетырёхугольнике противоположные углы попарно равны. докажите, что противоположные стороны четырехугольника попарно равны...
Флов227монстр Флов227монстр  02.08.2019 09:50
Величина одного из углов, при пересечении двух прямых, равна 44 градусам. найдите величины углов. 20 нужно...
Koley112 Koley112  05.06.2019 17:10
Поезд был задержан у семафора на 24 минуты и, чтобы прибыть на станцию назначения по расписанию, должен был оставшиеся 195 км проходить со скоростью, на 10 км/ч превышающей...
Kalibekova1 Kalibekova1  05.06.2019 17:10
Дан правильный треугольник с стороной 6. найдите высоту через теорему sin, cos и пифагора ....
MrDuster MrDuster  05.06.2019 17:10
Высота равнобедренного треугольника равна 3см ; а основание равно 8 см .найдите боковую сторону треугольника...
sonyabush12345 sonyabush12345  05.06.2019 17:10
Определить треугольный прямоугольник ?...
jeviduwel jeviduwel  24.10.2019 15:37
Доказать равенство углов, ! 7 класс...

Популярные вопросы