Дано: ABCD- параллелограмм BK перпендикулярно AD, CF перпен-но AD. Докажите, что площадь паралл-мма ABCD равна площади прямоугольника BKFC.
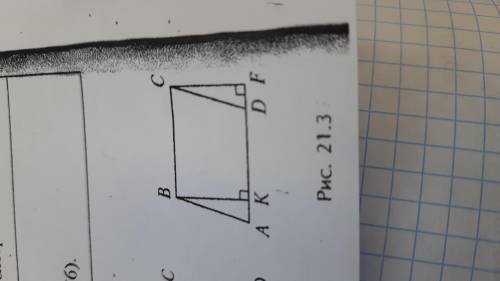
Другие вопросы по теме Геометрия
Популярные вопросы
- Название из букв: п,и,ч,а,л,л,п,а,а....
1 - Смысл пословицы. 1. любишь шутить над фомой, так люби и над собой. 2. смеется...
1 - Решите уравнения: 1 а) 5-2y=y+8 2 б) 1,2x+5,5=0,1x 3 в)12+7x=2x+15-13 4 г)...
3 - Какое число надо вписать в окошко ,что бы равенство 38/5=7+? /5. кот матроскин...
1 - Указать коэффициент выражения 2,6х*(-0,4)...
3 - Как это называется? ? прежде чем пахать землю, нужно было вырубать деревья,...
3 - 9-10 класс: назовите известных вам героев книг, которые не любили музыку!...
2 - Запишите число в виде периодической дроби а)-7/18 б)3/22 в)-2/27 г) -6/15...
2 - От одной пристани одновременно в противоположных направлениях отошли две лодки.одна...
2 - Из одного города в другой выехал поезд. первую половину расстояния он проехал...
2
1. Из условия задачи известно, что AB||CD и AD||BC. Это значит, что углы B и C являются соответственными и их междууроченная мера равна 180 градусам.
2. Согласно свойству параллелограмма, противоположные стороны равны по длине. Это значит, что AB = CD и AD = BC.
3. Также, согласно свойству параллелограмма, диагонали делят его на два равных по площади треугольника. Это значит, что площадь треугольника ABC равна площади треугольника CDA.
4. Из пункта 3 следует, что площадь параллелограмма ABCD равна удвоенной площади треугольника ABC (S_ABC = 2 * S_CDA).
Теперь рассмотрим прямоугольник BKFC.
5. Согласно свойству прямоугольника, его диагонали равны по длине и делят его на два равных по площади треугольника. Это значит, что площадь треугольника BKC равна площади треугольника CKF.
Теперь докажем, что S_ABC = S_BKFC.
6. Поскольку треугольники ABC и CDA равны по площади (из пункта 3), а треугольники BKC и CKF равны по площади (из пункта 5), то площадь треугольника ABC равна площади треугольника BKC, и площадь треугольника CDA равна площади треугольника CKF.
7. Дано, что BC||KF и AD||KF. Это значит, что углы BKC и CKF являются соответственными и их междууроченные меры равны 180 градусам.
8. Также, согласно свойству параллелограмма, противоположные стороны равны по длине. Это значит, что BK = CF и BC = KF.
9. Таким образом, треугольники BKC и CKF равны по площади и их основания равны (BK = CF) и высоты равны (BC = KF).
10. Таким образом, площадь треугольника BKC равна площади треугольника CKF.
Теперь можем заключить:
11. Площадь параллелограмма ABCD равна удвоенной площади треугольника ABC (S_ABC = 2 * S_CDA).
12. Площадь прямоугольника BKFC равна удвоенной площади треугольника BKC (S_BKFC = 2 * S_BKC).
Так как площади треугольников ABC и BKC равны (из пункта 6), то площадь параллелограмма ABCD равна площади прямоугольника BKFC (S_ABC = S_BKFC).
Таким образом, мы доказали, что площадь параллелограмма ABCD равна площади прямоугольника BKFC.