1. Геометрия
  2. Дано: abcd — параллелограмм,

Дано:
abcd — параллелограмм,
bc= 10 см, ba= 12 см,
∡ b равен 30°.

найти: площадь треугольника s(abc) и площадь параллелограмма s(abcd).

sδabc=
см2;

s(abcd)=
см2.

969696ааа 969696ааа    1   18.12.2019 22:53    6

Ответы
Romabl4 Romabl4  10.10.2020 21:39

Дано: ABCD — параллелограмм,

          BC = 10 см,  BA = 12 см,   ∠B = 30°

Найти : S_{\Delta ABC}\ ,\ S_{ABCD}

Площадь параллелограмма по формуле

S_{ABCD}=BC\cdot BA\cdot \sin \angle B=10\cdot 12\cdot \dfrac 12=60 см²

Диагональ параллелограмма AC делит его на два равных треугольника. То есть площадь треугольника ABC равна половине площади параллелограмма ABCD.

S_{\Delta ABC}=\dfrac 12 \cdot BC\cdot BA\cdot \sin \angle B=\dfrac 12\cdot 60=30 см²

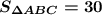ответ : \boldsymbol{S_{\Delta ABC}=30} см²;  \boldsymbol{S_{ABCD}=60} см²


Дано: abcd — параллелограмм, bc= 10 см, ba= 12 см, ∡ b равен 30°. найти: площадь треугольника s(abc
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Animeshon Animeshon  26.04.2020 16:08
Знайти площу рівнобедреного трикутника, бічна сторона якого 13 см і висота, проведена до основи- 5см.​...
dzavad1 dzavad1  26.04.2020 16:09
Площадь трапеции, изображённой на рисунке, равна 728, основание b=32, высота h=26. Найди второе основание трапеции​...
mozhena2000 mozhena2000  26.04.2020 16:09
На осі ординат знайдіть точку, рівновіддалена від точок А(4;-5) і В(2;3) На оси ординат найдите точку, равноудалена от точек А(4;-5) и В(2;3)...
feo073007feo feo073007feo  26.04.2020 16:09
№ 1. По рисунку сравните стороны СВ и АС, прямоугольного ∆АВС. Выберите и поставьте соответствующий знак: =, , . № 2. Какая из сторон треугольника самая большая? № 3....
БогданКК БогданКК  26.04.2020 16:10
До ть окрім 2 будь ласка. ​...
pazyny pazyny  26.04.2020 16:10
Стороны угла A касаются окружности с центром O радиуса R. Определи расстояние OA, если угол A=60 и R=32см...
SpecialCat SpecialCat  05.03.2021 10:36
ABCDA1B1C1D1 -прямоугольный параллелепипед. Назовите вектор, равный сумме векторов AD+D1C1-D1D+CB +В1А построить рисунок. , сор...
diana29102004 diana29102004  05.03.2021 10:36
Найдите неизвестные стороны и углы прямоугольного треугольника, если его катеты равны 10 и 10√3 см. На листочке с вложением и ответом...
Sarzhanovaperuza Sarzhanovaperuza  05.03.2021 10:35
знайдіть невідомий катет прямокутного трикутника якщо його гіпотенуза і другий катет відповідно лорівнюють 17 см і 8см...
мппьга мппьга  05.03.2021 10:34
В треугольнике ABC угол BAC равен 46 градусам. Найдите угол BCA, если внешний угол ABK этого треугольника равен 180 градусам ​...

Популярные вопросы