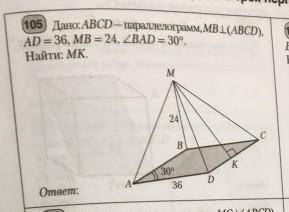
Дано abcd- паралеллограмм, mb перпендикулярна abcd, ad=36,mb=24, угол bad=30°,найти mk​

Для решения данной задачи, можно использовать свойства параллелограмма и теорему Пифагора.

1. Свойства параллелограмма:
- Противоположные стороны параллельны и равны.
- Противоположные углы параллельны и равны.

2. Обозначим точку пересечения прямых ad и bm как точку k.

3. Используя свойство параллелограмма, можем сделать следующие выводы:
- Строка mk - это высота параллелограмма, проведенная к основанию ab.
- Строка ad - это основание параллелограмма.
- Угол bad - это угол между основанием параллелограмма и высотой.
- Поэтому, треугольник abk находится внутри прямоугольного треугольника adm, где dm - это прямая, перпендикулярная к ab.

4. Известно, что ad=36 и угол bad=30°, и мы хотим найти mk, поэтому нам нужно найти mb, чтобы применить теорему Пифагора.

5. Для этого, используем свойство параллелограмма: mb || ad, поэтому угол amb равен углу mda.

6. В треугольнике amb есть две известные стороны: mb = 24 и ma = ad = 36. Мы также знаем угол amb, так как он равен углу bad.

Теперь можно воспользоваться теоремой Пифагора для нахождения mk:
- По теореме Пифагора: mk² = ma² - ak²

Чтобы найти ak, рассмотрим треугольник adm:
- Угол adm = 90° (так как треугольник abm является прямоугольным треугольником).
- Угол mad = bad = 30° (мы знаем, что угол mad = углу bad, так как mb || ad).
- Теперь мы можем использовать соотношение тангенса: tg(30°) = dm / ad
tg(30°) = dm / 36
(1/√3) = dm / 36
dm = 36/√3

Теперь, используя найденное значение dm, мы можем найти ak:
- Мы знаем, что синус угла mad = ak / dm
sin(30°) = ak / (36/√3)
(1/2) = ak / (36/√3)
ak = (36/√3) * 1/2
ak = 18/√3
ak = (18 * √3) / 3
ak = 6√3

Теперь мы можем найти mk:
- mk² = ma² - ak²
mk² = 36² - (6√3)²
mk² = 1296 - 36 * 3
mk² = 1296 - 108
mk² = 1188
mk = √1188
mk = √(4 * 3² * 33)
mk = √(4 * 9 * 33)
mk = √(4 * 297)
mk = √1188
mk = 2√297

Ответ: mk = 2√297.