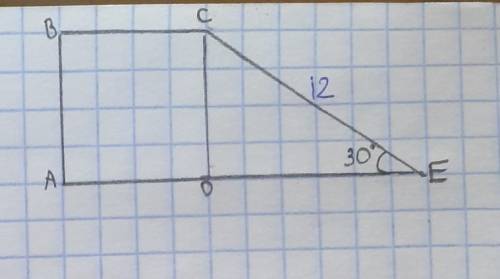
Дано:ABCD-квадрат CE=12 см угол CED=30 см.Найти Sabcd​

Чтобы найти площадь SABCD данного квадрата, мы можем использовать два различных подхода.

1) Мы можем разделить квадрат на два треугольника и найти сумму их площадей.

a) Найдем высоту треугольника CED. Мы знаем, что угол CED равен 30 градусов, а угол CDE равен 90 градусов (так как угол в квадрате всегда прямой). Зная эти углы, мы можем заключить, что треугольник CED является равносторонним треугольником (имеет равные стороны). Для нахождения высоты, мы можем разделить треугольник на два прямоугольных треугольника, и затем применить теорему Пифагора.

Итак, пусть h будет высотой треугольника CED. Так как треугольник CED равносторонний, то его сторона CE равна 12 см. Зная, что угол CED равен 30 градусов, мы можем найти h.

h = CE * sin(30)
h = 12 * sin(30)
h = 12 * 0.5
h = 6 см

b) Теперь мы можем найти площадь треугольника CED, используя формулу площади треугольника: Площадь = 0.5 * основание * высоту.

S_CED = 0.5 * CE * h
S_CED = 0.5 * 12 * 6
S_CED = 36 см²

c) Так как квадрат ABCD разделен на два треугольника, площадь квадрата равна сумме площадей двух треугольников.

SABCD = 2 * S_CED
SABCD = 2 * 36
SABCD = 72 см²

Таким образом, площадь квадрата ABCD равна 72 см².

2) Второй подход заключается в использовании формулы площади квадрата, основанной на длине его стороны.

a) У нас уже есть заданная длина стороны CE, которая равна 12 см. Найдем сторону квадрата ABCD, мы можем применить теорему Пифагора к треугольнику CDE.

Сторона CD = √(CE² + DE²)
CD = √(12² + 12²)
CD = √(144 + 144)
CD = √(288)
CD = 12√2 см

b) Так как квадрат ABCD имеет равные стороны, длина стороны AC также равна 12√2 см.

c) Теперь мы можем найти площадь квадрата ABCD, используя формулу площади квадрата: Площадь = сторона².

SABCD = AC²
SABCD = (12√2)²
SABCD = 12² * (√2)²
SABCD = 144 * 2
SABCD = 288 см²

Таким образом, площадь квадрата ABCD равна 288 см².

Оба подхода дали нам одинаковый ответ - 72 см². Вы можете выбрать любой из этих методов для решения этой задачи.