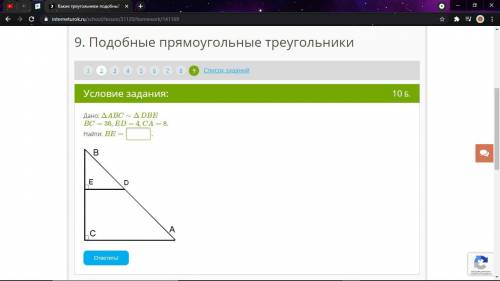
Дано: ΔABC∼ΔDBE
BC= 36, ED= 4, CA= 8.
Найти: BE=
.

ВЕ= 4см

Объяснение:

Но я не могу объяснить

Для решения данной задачи нам понадобится знание о пропорциональности сторон подобных треугольников.

Поскольку треугольники ΔABC и ΔDBE подобны, то соответствующие их стороны должны быть пропорциональны. То есть мы можем записать следующее равенство пропорций:

BC/BE = CA/ED

Подставим известные значения в данное уравнение:

36/BE = 8/4

Упростим его:

36/BE = 2

Чтобы найти BE, мы можем использовать свойство пропорций, согласно которому, если две дроби AB/CD = EF/GH, то их произведения AB*GH = CD*EF.

Применим это свойство к нашему уравнению:

36/BE = 2

36*2 = BE

72 = BE

Итак, пропорция свидетельствует о том, что BE должно быть равным 72.