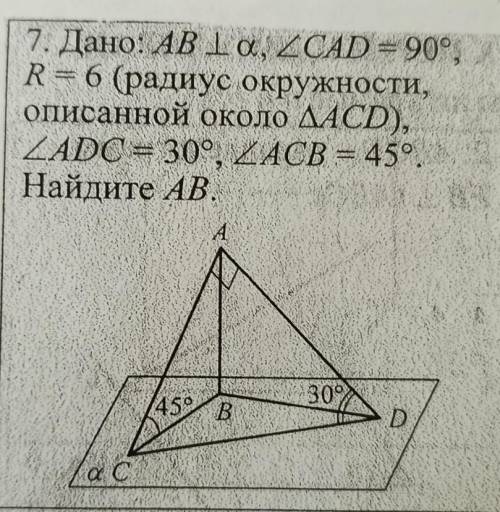
дано: AB перпендикулярно a, угол CAD = 90°, R = 6 (радиус окружности описанной около треугольника ACD), угол ADC = 30°, угол ACB = 45°. Найдите AB​

Чтобы решить эту задачу, нам понадобятся некоторые геометрические свойства и формулы. Давайте разберемся с каждым вопросом по порядку.

1. «AB перпендикулярно a» означает, что отрезок AB является перпендикуляром к прямой a. Перпендикулярные прямые образуют угол величиной 90°. Таким образом, угол CBA равен 90°.

2. Угол CAD равен 90°. Таким образом, треугольник CAD является прямоугольным.

3. R = 6 означает, что радиус окружности, описанной вокруг треугольника ACD, равен 6.

4. Угол ADC равен 30°. Этот угол является внутренним углом треугольника ACD, вписанным в окружность. Согласно теореме о вписанных углах, внутренний угол, образованный дугой, в два раза больше центрального угла, образованного той же дугой. Таким образом, центральный угол AOC, который соответствует дуге ADC, равен 60°. Значит, угол AOD также равен 60°.

5. Угол ACB равен 45°.

Теперь мы можем решить задачу.

1. Так как AB перпендикулярен a, то угол CBA равен 90°.

2. Треугольник CAD прямоугольный. Мы знаем угол CAD = 90°, поэтому угол ACD равен 180° - 90° = 90°.

3. Радиус окружности, описанной вокруг треугольника ACD, равен 6.

4. Угол ADC равен 30°. Так как это внутренний угол, образованный дугой, то центральный угол AOC, образованный той же дугой, равен 60°. Угол AOD также равен 60°.

5. Угол ACB равен 45°.

Теперь мы можем построить рисунок с учетом всех этих данных и найти значение AB.



Чтобы найти AB, нам понадобятся некоторые дополнительные геометрические свойства и формулы.

Из прямоугольного треугольника CAD мы знаем, что AC и CD являются катетами, а AD - гипотенузой. Согласно теореме Пифагора, сумма квадратов длин катетов равна квадрату длины гипотенузы.

AC² + CD² = AD²

Также, используя свойства треугольника AOX (где X - центр окружности, описанной вокруг треугольника ACD), мы можем найти длину AD.
В треугольнике AOC sin(ADС) = AD / AC (либо sin(30°) = AD / AC). Используя формулу sin(30°) = 1/2, мы можем записать это уравнение как 1/2 = AD / AC.

Теперь, чтобы решить систему уравнений, мы можем использовать выражение для AD, полученное из уравнения sin(30°)=1/2, и подставить его в уравнение АС² + СD² = AD².

AC² + CD² = (AC/2)²

AC² + CD² = AC²/4

Теперь мы можем упростить уравнение и продолжить решение:

CD² = AC²/4

CD = AC/2

Используя угол CAD = 90°, мы можем записать:

sin(90°) = CD / R,
sin(90°) = CD / 6,
1 = CD / 6,
CD = 6.

Теперь мы можем найти значение AB, используя угол ACB = 45°:

cos(45°) = AB / CD,
cos(45°) = AB / 6,
AB = 6 * cos(45°),
AB = 6 * (√2 / 2),
AB = 3√2.

Итак, AB = 3√2.

Угол АСД=60°
Напротив угла 30° лежит 1/2 гипотенузы =>3
Треугольник абс равнобедренный тк аб перпендикулярно (СВД) =>аб=3