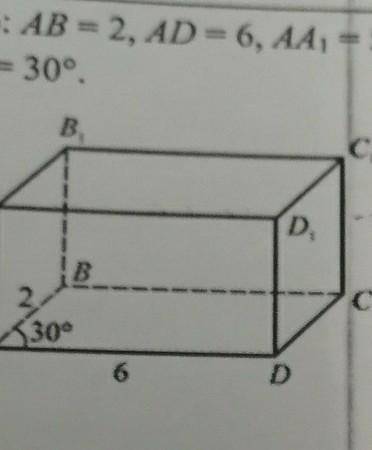
Дано: AB=2 AD=6 AA1=5 <BAD=30°
Найти:V параллелепипеда-?​

Для начала построим параллелограмм ABCD по данному условию:

Первый шаг:
AB = 2 (дано)
AD = 6 (дано)
Угол BAD = 30° (дано)
Мы знаем, что угол BAC (или угол BAD) равен углу BDA (или углу BCD) (свойство параллелограмма).
Поэтому угол BDA (или BCD) тоже равен 30°.

Второй шаг:
Для вычисления площади параллелограмма ABCD, нам нужно найти высоту параллелограмма.
Высота параллелограмма - это перпендикуляр, опущенный от вершины A на основание CD.

Третий шаг:
С помощью тригонометрических соотношений, можем найти высоту параллелограмма.
В треугольнике BAD прямоугольного угла B содержит угол в 30° и прямые катеты AB и AD.
Мы можем найти противоположный катет (высоту) при помощи тригонометрии:
tan(30°) = противоположный катет / прилежащий катет
tan(30°) = высота / AB
1/√3 = высота / 2
высота = 2/√3

Четвертый шаг:
Вычислим площадь параллелограмма ABCD, используя формулу S = основание * высота.
В данном случае, основание CD равно AD = 6.
Площадь = 6 * (2/√3) = 12/√3

Пятый шаг:
Чтобы найти объем параллелепипеда, мы должны найти высоту параллелепипеда, которая равна высоте параллелограмма. Затем умножаем высоту на площадь основания.

Шестой шаг:
У нас есть площадь основания и высота параллелепипеда, которую мы только что вычислили. Поэтому, V = S * h = (12/√3) * (2/√3) = 24/9 = 8/3.

Ответ:
V параллелепипеда равен 8/3.