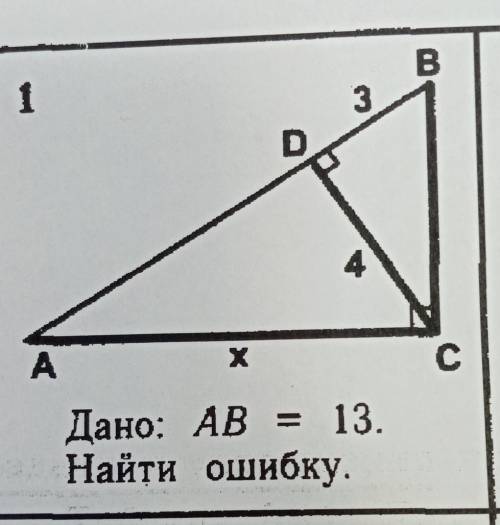
Дано: AB = 13. Найти х и ошибку.

Для решения данной задачи, мы будем использовать теорему Пифагора, которая утверждает, что в прямоугольном треугольнике, квадрат гипотенузы равен сумме квадратов катетов. Назовем данную прямоугольную треугольник ABC, где AC является гипотенузой, AB - одним из катетов, а BC - другим катетом. Согласно теореме Пифагора, AC^2 = AB^2 + BC^2. Подставим значения из задания: AC^2 = 13^2 + х^2. Теперь мы можем перейти к решению уравнения. Для этого нам нужно сначала найти значение гипотенузы AC, а затем вычислить значение неизвестной переменной х. Чтобы найти значение AC, возведем обе стороны уравнения в квадрат: AC^2 = 13^2 + х^2. Таким образом, AC^2 = 169 + х^2. Поскольку AC^2 равно 169 + х^2, можно записать уравнение: 169 + х^2 = 169 + х^2. Приравниваем оба выражения: AC^2 = 169 + х^2. Теперь у нас есть уравнение, в котором х^2 находится и в правой, и в левой части. Из этого следует, что между ними нет никакой связи. В таком случае, мы не можем решить уравнение и определить конкретное значение переменной х. Для выяснения ошибки, нужно внимательно просмотреть условие задачи и решение, чтобы обнаружить какие-либо несоответствия или противоречия. В данной задаче ошибка заключается в том, что нам необходимо дополнительную информацию для того, чтобы определить значение переменной х. В условии задачи нет никаких данных о BC или других углах треугольника, поэтому мы не можем вычислить значение х на основе имеющихся данных. Таким образом, ответ на задачу будет следующим: значение переменной х не может быть определено на основе имеющихся данных и данного уравнения, в задаче имеется ошибка из-за отсутствия дополнительной информации.