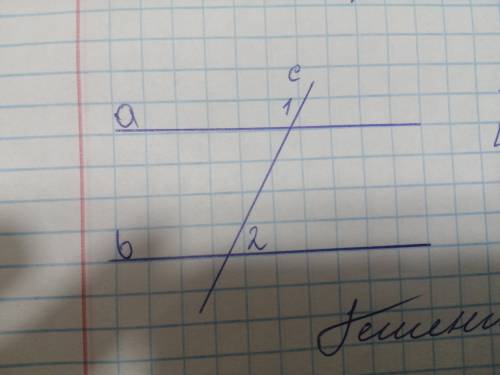
Дано A//B, c-секущая

угол 1 + угол 2 = 122 найти все обо, углы

Для решения задачи нам понадобятся знания о свойствах параллельных линий и о свойствах углов при пересечении секущими.

Дано, что AB параллельна CD, а AC - секущая.

Угол 1 и угол 2 являются вертикальными углами и, по свойству вертикальных углов, они равны друг другу. Поэтому, угол 1 = угол 2.

Также, оба угла 1 и 2 образованы пересечением секущей AC с параллельными линиями AB и CD. По свойству углов при пересечении секущими, сумма углов 1 и 2 должна быть равна 180 градусов.

Из условия задачи, угол 1 + угол 2 = 122. Подставляем это значение в уравнение и решаем его:

угол 1 + угол 2 = 122
2 * угол 1 = 122
угол 1 = 122 / 2
угол 1 = 61

Так как угол 1 = угол 2, то угол 2 также равен 61 градус.

Таким образом, ответом на задачу является то, что угол 1 и угол 2 равны 61 градус.