Дано :
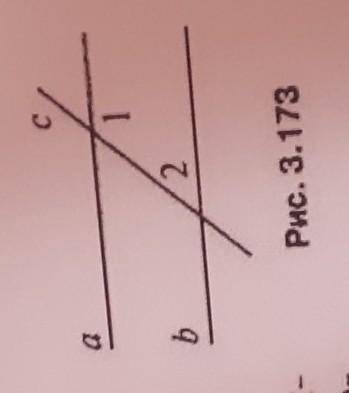
a||b , c-секущая,
угол 1 - угол 2=102°
Найти: все образовавшиеся углы.​

1) 102:2=51- угол 1

2) 180-51=129- угол 2

Для решения этой задачи, нам понадобится использовать свойство параллельных прямых, секущих и углов.

Исходя из доказательства, угол 1 - угол 2 = 102° образуется при прямопропорциональном пересечении трех прямых. В данном случае, это параллельные прямые a и b, а также секущая c.

Поскольку a||b, мы знаем, что углы 1 и 2 соответственно равны.

Обозначим углы, образовавшиеся после пересечения c с a и b, как углы 3 и 4 соответственно (см. рисунок).

Таким образом, углы 3 и 4 также равны между собой.

Итак, чтобы найти все образовавшиеся углы, нам нужно найти значения углов 1, 2, 3 и 4.

Давайте решим задачу пошагово:

Шаг 1: Углы 1 и 2 равны, так как a||b и они соответственные.
Угол 1 = Угол 2 (свойство соответственных углов)
Угол 1 - Угол 2 = 0 (вычитание равных углов)
Таким образом, угол 1 - угол 2 = 0°.

Шаг 2: Угол 1 - угол 2 = 0°, но по условию равен 102°.
Это означает, что 0° + 102° = 102°.

Шаг 3: Угол 3 и угол 4 равны между собой, так как они корреспондентные.
Угол 3 = Угол 4 (свойство корреспондентных углов)

Шаг 4: Угол 1 - угол 3 = Угол 2 - угол 4 = 102°.
Это свойство прямопропорционального пересечения трех прямых.

Итак, все образовавшиеся углы равны:
Угол 1 = Угол 2 = 102°
Угол 3 = Угол 4 = 0°

Надеюсь, это будет полезно для понимания решения задачи. Если у вас возникнут еще вопросы, не стесняйтесь задавать.