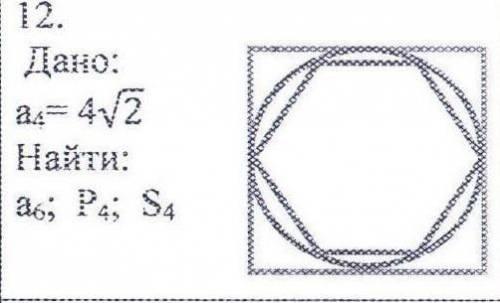
Дано:
a⁴=4√2
Найти:
a⁶, P⁴, S⁴​

Для шестиугольника данная окружность описанная, а для квадрата--вписанная. Приравняем формулы для радиуса этой окружности
R=a6
r=a4/2
a6=a4/2=(4√2)/2=2√2
P4=4*a4=4*4√2=16√2
S4=(a4)²=(4√2)²=16*2=32 кв.ед.

Для решения данной задачи, нам нужно применить основные математические операции и правила возведения в степень.

Первое, что мы можем заметить, это то, что дана степень числа a в четвертой степени равна 4√2. Это означает, что a⁴ = 4√2.

Теперь мы должны найти a⁶, P⁴ и S⁴.

1. Нахождение a⁶:
Чтобы найти a⁶, мы можем возвести a в шестую степень:
a⁶ = (a⁴)², поскольку потребуется использовать основное свойство возведения в степень, которое гласит "степень степени равна умножению степеней".
Подставляя значение a⁴ = 4√2 в формулу, получаем:
a⁶ = (4√2)² = 4² * (√2)² = 16 * 2 = 32.

Таким образом, a⁶ = 32.

2. Нахождение P⁴:
Для нахождения P⁴, мы должны вычислить периметр квадрата и возвести его в четвертую степень.
Периметр квадрата P равен сумме всех его сторон: P = a + a + a + a = 4a.
Таким образом, P⁴ = (4a)⁴. Применяя свойство возведения в степень, имеем:
P⁴ = 4⁴ * a⁴ = 256 * a⁴.
Значение a⁴ дано в условии и равно 4√2, подставляя его в формулу, получаем:
P⁴ = 256 * 4√2 = 1024√2.

Таким образом, P⁴ = 1024√2.

3. Нахождение S⁴:
Для нахождения S⁴, мы должны вычислить площадь квадрата и возвести ее в четвертую степень.
Площадь квадрата S равна произведению его стороны: S = a * a = a².
Таким образом, S⁴ = (a²)⁴. Применяя свойство возведения в степень, имеем:
S⁴ = a⁴ * a⁴. Значение a⁴ дано в условии и равно 4√2.
Подставляя это значение в формулу, получаем:
S⁴ = (4√2) * (4√2) = 16 * 2 = 32.

Таким образом, S⁴ = 32.

В итоге, мы нашли:
a⁶ = 32,
P⁴ = 1024√2,
S⁴ = 32.