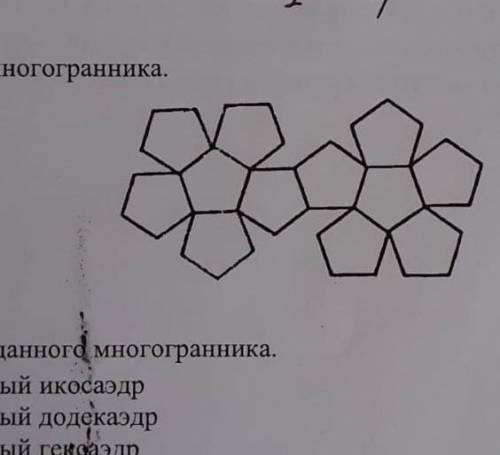
Дана развертка многогранника
укажите количество вершин и вид многоугольника​

Данная развертка представляет собой многогранник, который является призмой.

Многогранник состоит из двух правильных пятиугольных оснований, которые образуют верхнюю и нижнюю плоскости, и прямоугольных граней, которые соединяют основания.

Теперь рассмотрим количество вершин многогранника.
- Каждое пятиугольное основание имеет 5 вершин.
- У прямоугольных граней есть две вертикальные ребра, по одному на каждом конце. Это добавляет еще 2 вершины.
- На концах многогранника также видны две дуги, каждая из которых имеет одну вершину.

Итого, общее количество вершин равно 5 (вершины пятиугольного основания) + 2 (вершины на ребрах прямоугольных граней) + 2 (вершины на концах многогранника) = 9 вершин.

Таким образом, количество вершин в данном многограннике равно 9.