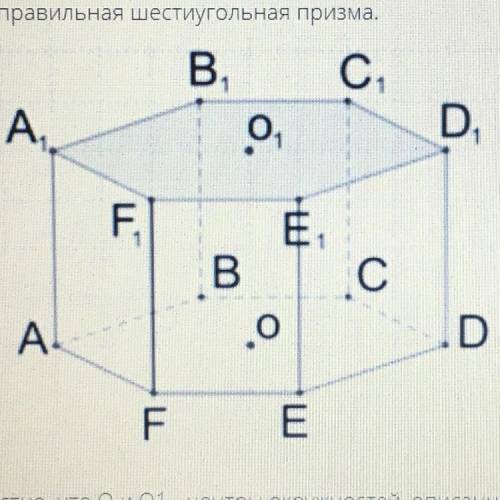
Дана правильная шестиугольная призма. Известно, что О и О1 - центры окружностей, описанных около оснований. Длина вектора AF равна 5, площадь BB1D1D=60 корней из 3. Найдите длину вектора AO1

Для решения этой задачи, давайте разберемся пошагово.

Шестиугольная призма имеет два основания, которые являются правильными шестиугольниками. Означает, что все стороны и углы оснований равны между собой.

Первое, что нам нужно сделать, это изобразить данную ситуацию на чертеже:

A — верхняя вершина призмы
B и C — вершины одного из оснований
B1 и C1 — вершины другого основания
D и D1 — серединные точки соответствующих сторон оснований (на чертеже их не отмечено)
О и О1 — центры окружностей, описанных около оснований

Мы также имеем два вектора: AF и AO1.

Давайте вначале найдем длину сторон основания. Так как шестиугольник правильный, все его стороны равны. Пусть сторона шестиугольника равна a.

Так как AO и AO1 - радиусы окружностей, описанных около оснований, то они равны длине стороны шестиугольника. То есть AO = AO1 = a.

Стоит заметить, что вершина A и центр окружности О1 лежат на одной вертикали из-за симметрии фигуры. Это означает, что вертикальный отрезок от вершины А до основания должен быть перпендикулярен к основанию. Обозначим середину основания данного отрезка D1.

Мы также знаем, что площадь BB1D1D = 60корень из 3. Так как D и D1 - серединные точки соответствующих сторон оснований, то площадь BB1D1D = 2 * площадь BCD. Обозначим площадь BCD как S.

S = 60корень из 3 / 2 = 30корень из 3

Площадь правильного шестиугольника можно найти по формуле:

S = (3 * корень из 3 * a^2) / 2

30корень из 3 = (3 * корень из 3 * a^2) / 2

Упростим уравнение, избавившись от корня из 3:

60 = 3a^2

a^2 = 20

a = квадратный корень из 20

Так как AO1 = a, то AO1 = a = квадратный корень из 20.

Итак, длина вектора AO1 равна квадратному корню из 20.