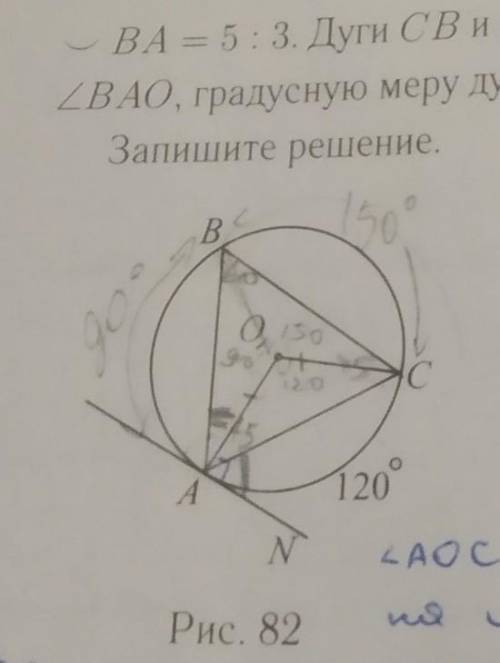
Дана окружность с центром в точке О, АN- касательная, CB и CA- хорды. известно что дуга AC= 120° дуга CB : дугу BA в соотношении 5:3. дуги CB и BAменьше 180. найдите у. АОС у. АБС, у.САN, у БАО, градусную меру дуг Аб и Бс. итак, я нашла все, кроме углов CAN и

( аос- 120, абс- 60, дуга аб- 90, дуга бс- 150)​

Чтобы решить эту задачу, мы можем использовать несколько свойств окружности и треугольников.

1) Угол между касательной и хордой, проведенной из точки касания, всегда равен углу, натянутому на эту хорду относительно центра окружности. Таким образом, угол АОС равен половине градусной меры дуги AC, то есть 120° / 2 = 60°.

2) Угол, внутри круга и натянутый на хорду, равен половине меры дуги, заключенной между этой хордой и другой хордой, начинающейся и заканчивающейся на той же стороне относительно первой хорды. Таким образом, угол АБС равен половине меры дуги CB, которая составляет 5/8 от полной окружности, то есть 5/8 * 360° = 225° / 2 = 112.5°.

3) Угол, внутри круга и натянутый на ту же хорду, что и другой угол, равен половине меры дуги, заключенной между этой хордой и другой хордой, заканчивающейся на противоположной стороне относительно первой хорды. Таким образом, угол САN равен половине меры дуги CB, которая составляет 3/8 от полной окружности, то есть 3/8 * 360° = 135° / 2 = 67.5°.

4) Угол АОВ равен 180° - углу АОС, то есть 180° - 60° = 120°.

5) Угол ВСА равен углу АБС, так как они натянуты на одну и ту же хорду AB.

Таким образом, мы находим все углы:

АОС = 60°
АБС = 112.5°
САN = 67.5°
БАО = 120°
АОВ = 120°
ВСА = 112.5°

Теперь давайте найдем градусные меры дуг AB и BC.

Угол АБС равен половине меры дуги CB, которая составляет 5/8 от полной окружности. То есть мера дуги CB равна 5/8 * 360° = 225°. Таким образом, мера дуги AB равна 360° - 225° = 135°.

Угол ВСА равен половине меры дуги CB, которая составляет 3/8 от полной окружности. То есть мера дуги CB равна 3/8 * 360° = 135°. Таким образом, мера дуги BC равна 360° - 135° = 225°.

Итак, найденные градусные меры дуг:

Дуга AB = 135°
Дуга BC = 225°

Надеюсь, это решение понятно для вас! Если у вас есть еще вопросы, не стесняйтесь задавать!