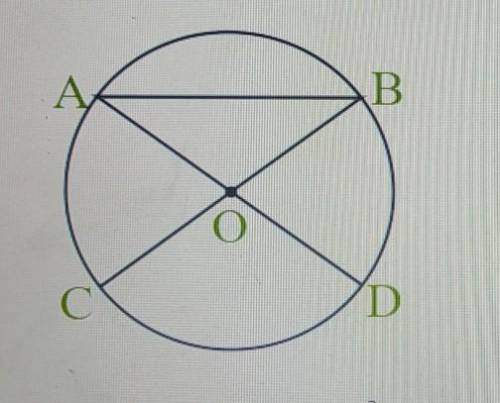
Дана окружность с центром О, через который проходят две хорды. Найдите угол DAB, если угол COD = 73°. Запишите только числовое значение.​

угл cod=углу aob, как вертикальные, угл adb=86. треугольник aob равнобедренный ao=bo, так как угл dab= углу abc=(180-73):2=53,5 угл abc=53,5

Для решения этой задачи, нам понадобятся некоторые свойства окружностей и пропорциональные углы.

1. Самое важное свойство, которое мы будем использовать, - это то, что центральный угол, охватывающий дугу, равен удвоенному соответствующему периферийному углу. То есть, если угол COD равен 73°, то угол при ЦОД будет равен половине этого значения, то есть 73°/2 = 36.5°.

2. Мы также будем использовать свойство углов, образуемых хордами, пересекающимися внутри окружности. Если дуги AB и CD пересекаются внутри окружности, то угол DAB будет равен половине суммы дуг AD и BC.

Теперь поглядим на заданную диаграмму и посмотрим, какую информацию мы можем использовать для решения задачи.

У нас дана окружность с центром О, через который проходят две хорды OC и OD. Кроме того, задан угол COD, равный 73°. Отметьте, что хорды OC и OD делят окружность на четыре дуги: AB, AC, BD и CD.

Согласно свойству №1, мы знаем, что угол при ЦОД равен половине заданного угла COD, то есть 73°/2 = 36.5°. Теперь взглянем на треугольник ОCD. Мы знаем, что сумма углов треугольника равна 180°, поэтому можем записать уравнение:

угол О + угол ОСД + угол ОДС = 180°.

Угол ОСД и угол ОДС являются периферийными углами к хордам OD и OC, поэтому каждый из них равен половине угла при ЦОД, то есть 36.5°/2 = 18.25°.

Теперь можем переписать уравнение:

угол О + 18.25° + 18.25° = 180°.

Сложим 18.25° + 18.25° = 36.5° и вычтем это значение из обоих сторон уравнения:

угол О = 180° - 36.5°.

угол О = 143.5°.

Мы нашли угол при вершине центрального угла, теперь мы можем найти угол DAB, используя свойство №2. Поскольку хорда OD содержит дугу AD, а хорда OC содержит дугу BC, сумма дуг AD и BC равна дуге CD. Из диаграммы видно, что дуга CD равна 73°.

Следовательно, угол DAB равен половине суммы дуг AD и BC, то есть 73°/2 = 36.5°.

Таким образом, угол DAB равен 36.5°.