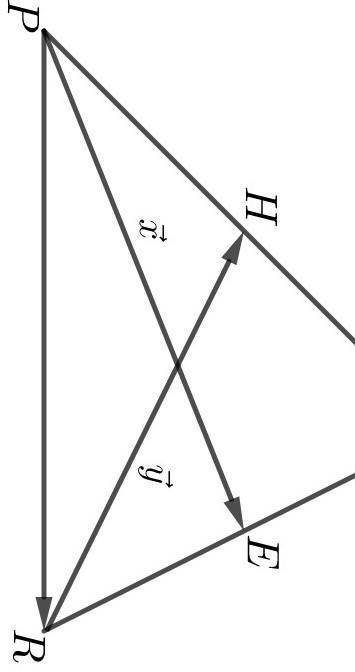
Дан треугольник PRQ. Пусть H и E - середины сторон PQ и QR соответственно. Известно,что вектор PE = вектору x и вектор RH = вектору y Выразите вектор PR через векторы x и y
Другие вопросы по теме Геометрия
Популярные вопросы
- 1.постройте график функции y=4-2x. используя построенный график, ответьте...
3 - Напишите улицы мелиораторов, город городец...
2 - Сочинение по симфонии номер пять первый вопрос кого или что вы представляете...
3 - Вмастерской израсходовали 320 м шерсти и 340 м льна на пошив костюмов....
3 - Надо сделать рассказ про запоминающийся день в школе(на ) желательно с...
2 - Подчеркни в нём главные члены над каждым словом напеши какой частью речи...
1 - Circle the correct sentence. 1.we celebrate april fool s day in april...
2 - Составить сочинение на тему весна по опорным словам: весна,воздух,ручьи,ледоход,в...
1 - Моторная лодка по течению проплыла за 5 часов такое же расстояние,как...
1 - Проведите наблюдения за движениями собаки или кошки, когда животное бегает,...
2
1. По свойству серединного перпендикуляра, вектор PE будет перпендикулярен стороне QR и его длина будет равна половине длины стороны QR. Аналогично, вектор RH будет перпендикулярен стороне PQ и его длина будет равна половине длины стороны PQ.
2. Обозначим длину стороны QR как a и длину стороны PQ как b. Тогда длина вектора PE будет равна a/2, а длина вектора RH будет равна b/2.
3. Поскольку векторы PE и x равны, мы можем записать их координаты как (a/2, 0).
4. Аналогично, векторы RH и y равны, поэтому их координаты будут (0, b/2).
5. Теперь мы можем записать координату вектора PR как сумму координат векторов PE и RH. Это можно сделать, складывая соответствующие координаты: (a/2 + 0, 0 + b/2), что дает нам вектор (a/2, b/2).
6. Таким образом, вектор PR будет иметь координаты (a/2, b/2), что в итоге означает, что вектор PR выражается через векторы x и y следующим образом: PR = (a/2, b/2).
Итак, мы нашли выражение для вектора PR, используя данные о векторах x и y.