Дан треугольник АВС, в котором АС=4, ВС=7, АВ=6 найдите cos ABС
Другие вопросы по теме Геометрия
Популярные вопросы
- Синтаксический разбор предложения: Владимир и писал бы оды, да Ольга не...
3 - При яких значеннях x вираз має зміст: ✓2x+5+✓2-x...
2 - Просвітницькі напрямки які бувають?...
2 - Какие страны начали первые плавать?...
1 - Поміркуйте, яку користь е від тварин-сусідів і якої шкоди окремі види...
3 - Написать тест как часть речи верю не верю 10 вопросов....
1 - Автомобіль проїхав половину шляху зі швидкістю 60км/год; половину часу,...
2 - Дано:ABCD прямокутна трапеція, BC =12см, AD=18см, DB -діагональ, що ділить...
3 - 9 предложений вопросительны,относительны,отрицательны...
3 - УЧЕНИЕ БЕЗ МУЧЕНИЯ Что же нужно делать, чтобы учение не стало мучением?...
2
Угол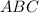 для краткости обозначим за
для краткости обозначим за 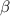 .
.
Тогда, по теореме косинусов, верно следующее:
Подставляем все известное в уравнение:
Косинус угла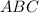 найден!
найден!