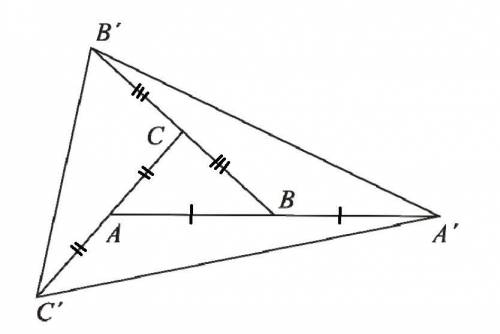
Дан треугольник ABC. Точка A' лежит на продолжении стороны AB так, что AB = BA', точка B' лежит на продолжении стороны BC так, что BC = CB', точка C' лежит на продолжении стороны CA так, что CA = AC'. Во сколько раз площадь треугольника A'B'C' больше площади треугольника ABC?

Вариант ответа.

ответ: В 7 раз. .

Объяснение: Площади треугольников, имеющих одинаковую высоту, относятся как основания, к которым проведена эта высота. Следовательно, площади треугольников с равными основаниями и общей высотой равны.

   Рассмотрим треугольник АВС и АВ1С . Основания этих треугольников равны ( СВ1=СВ по условию), высота из вершины А у них общая.  => Площади этих треугольников равны.

Аналогично площади ∆ ВСА1 и ∆ ВАС1  равны площади ∆ АВС.

  Рассмотрим треугольники АВ1С1 и АСВ1. Они имеют равные основания ( АС=АС1 по условию) и общую высоту из В1.

Ѕ ∆ АС1В1= Ѕ ∆АВ1С=Ѕ(АВС)

По тем же основаниям Ѕ ∆ СА1В1=Ѕ ∆ ВСА1=Ѕ(АВС) и

Ѕ ВС1А1=Ѕ АВС1=Ѕ ∆ АВС.

Следовательно.

Ѕ ∆ АВ1С1=2Ѕ (АВС)

Ѕ ∆ ВВ1А1=2Ѕ(АВС)

Ѕ ∆ АС1А1=2Ѕ(АВС) =>

Ѕ (А1В1С1) равна сумме площадей семи равновеликих треугольников.

Ѕ (А1В1С1):Ѕ(АВС)=7

sin(α) = sin(180° - α)

1) S(ABC) = 0,5·AB·BC·sin(∠ABC),

S(A'BB') = 0,5·A'B·BB'·sin(∠A'BB') = 0,5·AB·2BC·sin(180° - ∠ABC) =

= AB·BC·sin(∠ABC) = 2·S(ABC)

2) S(ABC) = 0,5·AC·AB·sin(∠BAC)

S(AC'A') = 0,5·AC'·AA'·sin(∠C'AA') = 0,5·AC·2AB·sin(180° - ∠BAC) =

= AC·AB·sin(∠BAC) = 2·S(ABC).

3) S(ABC) = 0,5·AC·BC·sin(∠ACB)

S(B'CC') = 0,5·B'C·CC'·sin(∠B'CC') = 0,5·BC·2AC·sin(180° - ∠ACB) =

= BC·AC·sin(∠ACB) = 2·S(ABC).

Итак, S(A'B'C') = S(ABC) + S(A'BB') + S(AC'A') + S(B'CC') =

= S(ABC) + 2S(ABC) + 2S(ABC) + 2S(ABC) = 7·S(ABC).

ответ. В 7 раз.