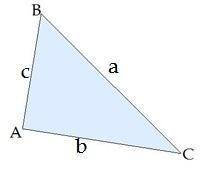
Дан треугольник ABC. AC= 27 см;
∢ B= 30°;
∢ C= 45°.
(ответ упрости до наименьшего натурального числа под знаком корня.)
ответ: AB= −√ см
Другие вопросы по теме Геометрия
Популярные вопросы
- Окаком событии написаны следующие строки....
1 - Велосипедист проехал 27 км по шоссе из а в в. возвращался он по просёлочной...
3 - Перестройте предложение, используя страдательный залог. he will pay for flowers...
1 - Вычислительные массу раствора серной кислоты с массовой долей вещества 15%,...
2 - Расставьте знаки препинания, укажите вид глаголов и деепричастий . кроме готовых...
3 - Какое влияние имело андрусовское перемирие на запорожье...
2 - Составте рассказ на свободную тему с употреблением местоимениями...
1 - Определите тип условного предложения: 1) if isn t rain, the plants die 2) if...
3 - Составьте вопросительное предложение 1. the smiths have got two cars. 2. they...
1 - 1. look at the language focus. translate the time connectors into your language...
1
Для начала, мы знаем, что в треугольнике сумма всех трех углов равна 180°. Таким образом, угол A равен:
∢ A = 180° - ∢ B - ∢ C
∢ A = 180° - 30° - 45°
∢ A = 180° - 75°
∢ A = 105°
Теперь мы можем использовать закон синусов, чтобы найти длину стороны AB. Закон синусов гласит:
AB/sin(∢ A) = AC/sin(∢ C)
Заменим значения:
AB/sin(105°) = 27/sin(45°)
Теперь найдем sin(105°) и sin(45°). Но сначала нам потребуется найти sin(180° - 105°), потому что sin(x) = sin(180° - x):
sin(180° - 105°) = sin(75°)
Таким образом, мы можем переписать уравнение:
AB/sin(75°) = 27/sin(45°)
Теперь найдем значения sin(75°) и sin(45°):
sin(75°) = sin(30° + 45°)
Здесь нам пригодится формула синуса суммы:
sin(30° + 45°) = sin(30°)cos(45°) + cos(30°)sin(45°)
Теперь мы можем использовать значения синусов и косинусов 30° и 45°:
sin(30° + 45°) = (1/2)(√2/2) + (√3/2)(√2/2)
sin(30° + 45°) = (√2/4) + (√6/4)
sin(30° + 45°) = (√2 + √6)/4
Теперь мы можем переписать уравнение:
AB/((√2 + √6)/4) = 27/((√2)/2)
Теперь будем находить AB. Умножим обе стороны уравнения на (√2 + √6):
AB = (27/((√2)/2)) * ((√2 + √6)/4)
AB = (27*2*(√2 + √6))/(2*4*(√2))
AB = (27*(√2 + √6))/(8*(√2))
AB = (27*(√2 + √6))/(8*√2)
AB = (27*(√2 + √6))/(8√2)
AB = (27/8)*(√2/√2 + √6/√2)
AB = (27/8)*(1 + (√6/2))
Теперь упростим ответ до наименьшего натурального числа под знаком корня:
AB = (27/8)*(1 + (√6/2))
AB = (27/8) + (9/8)*√6
Таким образом, ответ упрощен до наименьшего натурального числа под знаком корня: AB = -√6 см.