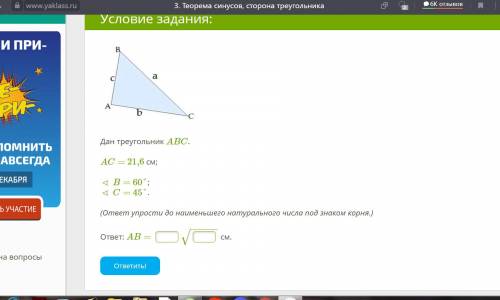
Дан треугольник ABC.

AC= 21,6 см;
∢ B= 60°;
∢ C= 45°.

(ответ упрости до наименьшего натурального числа под знаком корня.)
ответ: AB= _√__ см.

Для нахождения стороны AB в треугольнике ABC можно воспользоваться теоремой синусов. Согласно этой теореме, отношение длины каждой стороны треугольника к синусу противолежащего ей угла равно.

Таким образом, мы можем записать следующее соотношение:

AB / sin(∢ B) = AC / sin(∢ C)

Подставляем известные значения:

AB / sin(60°) = 21,6 / sin(45°)

Чтобы упростить решение, нам понадобится значение синусов 60° и 45°.

sin(60°) = √3 / 2
sin(45°) = √2 / 2

Подставляем их в уравнение:

AB / (√3 / 2) = 21,6 / (√2 / 2)

Упрощаем уравнение, домножая обе части на 2 и деля на √3:

AB * 2 / √3 = 21,6 * 2 / √2

Домножаем числитель и знаменатель на √3:

AB * 2 * √3 / 3 = 21,6 * 2 * √3 / √2

Упрощаем уравнение:

AB * √3 / 3 = 21,6 * √6

Домножаем числитель и знаменатель на 3:

AB * √3 = 21,6 * √6 * 3

AB * √3 = 64,8 * √6

Делим обе части уравнения на √3:

AB = (64,8 * √6) / √3

Домножаем числитель и знаменатель на √3:

AB = (64,8 * √6 * √3) / (√3 * √3)

AB = (64,8 * √18) / 3

Поскольку 18 = 9 * 2 и √9 = 3, упрощаем выражение:

AB = (64,8 * 3√2) / 3

Сокращаем числитель и знаменатель на 3:

AB = 64,8 * √2

AB ≈ 91,5 см

Итак, сторона AB треугольника ABC равна приблизительно 91,5 см.